Trans-formare = mutare conservando un’identità
( anche calcolare è trasformare: un’espressione, una formula)
Questioni Spinose
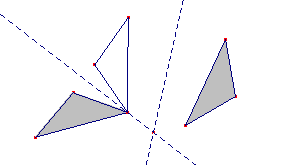
Sono la stessa figura ?
b è la stessa di a traslata
c è la stessa di a traslata e ruotata
d è la stessa di a traslata, ruotata, dilatata
Infine sono tutte un’unica fugura: il segmento orientato.
Le figure
geometriche sono parte (insieme di punti ) del piano (spazio) ma ….
Sono la stessa figura ? hanno una comune identità ?
Dilatando lungo una direzione
Importante è vedere la figura come un "pieno" e quindi la T.G. tra punti.
Proiettando oppure comprimendo lungo una direzione
invecchiando…
(stessa) identità = equivalenza rispetto a una classe di trasformazioni
Le isometrie non cambiano: forma, grandezza; cambiano:
Le similitudini non cambiano: forma; cambiano:
Le affinità (es.: ombre solari) non cambiano: parallelismo, rapporti tra aree, limitato/illimitato; cambiano: perpendicolarità, forma
Le proiettività) (es.: prospettiva, ombre) non cambiano allineamento, n° vertici; cambiano: limitato/illimitato
Le trasformazioni topologiche (es. specchi deformanti, ombre su superfici non piane,..), non cambiano dentro/fuori, n° "buchi, strappi"
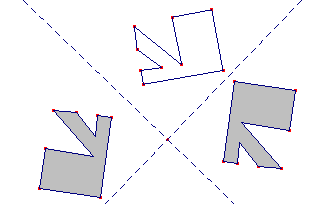
(Un puzzle è un esempio di trasformazione del piano che cambia tutto)
Trasformando lo spazio con una certa trasformazione non vediamo alcuna differenza in quell’ottica geometrica tra la figura e la sua immagine
Le isometrie non distinguono segmenti orientati con la stessa lunghezza: dati due segmenti orientati con la stessa lunghezza ce n’è sempre una e una sola che trasforma il primo nel secondo.
Le similitudini non distinguono segmenti orientati: dati due segmenti orientati ce n’è sempre una e una sola che trasforma il primo nel secondo, in particolare tutti i quadrati sono uguali
Le affinità non distinguono triangoli (né parallelogrammi): dati due triangoli ce n’è sempre una che trasforma uno nell’altro.
Le collineazioni non distinguono quadrilateri neanche da "angoli senza punta"
Le trasformazioni topologiche non distinguono tra figure senza tagli, con lo stesso n° di buchi…
|
Proprietà’ che persistono dopo i cambiamenti |
Esempi di figure |
classe di trasformazioni |
Tipo di geometria |
|
metriche lunghezza, distanza, grandezza |
Il triangolo equilatero di lato tot, il cerchio di raggio tot |
isometrie |
|
|
geometriche principali rapporto tra distanze, angoli, perpendicolarità, forma |
Il triangolo equilatero, il cerchio |
similitudini |
Geometria Euclidea |
|
affini parallelismo, rapporto tra le aree |
Il triangolo, il cerchio |
affinità |
Geometria affine |
|
proiettive allineamenti, centro di simmetria |
Parte di piano tra tre rette, la conica |
proiettività |
Geometria Proiettiva |
|
topologiche interno, n° di "buchi" |
Figura senza "buchi" |
trasf. topologiche |
Topologia |
Su, giù, sopra, sotto, destra, sinistra … non sono proprietà geometriche
Non esiste il triangolo isoscele, il rettangolo
Isometrie ( o congruenze) = Movimenti rigidi anche fuori del piano
Equiestensione (tutte le figure con il tangram hanno la stessa area)
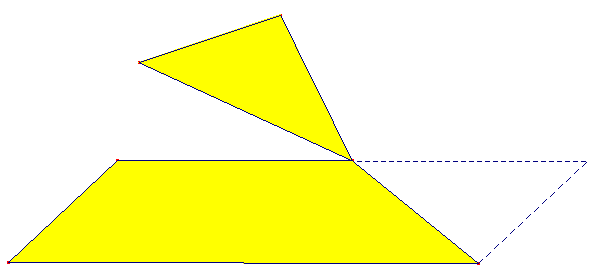
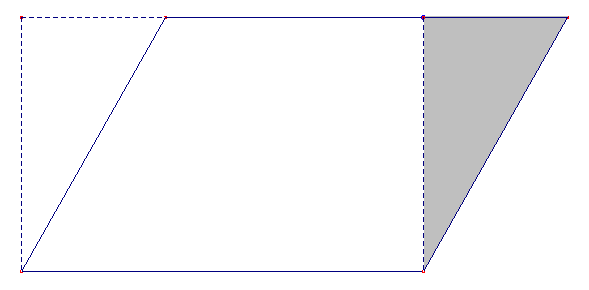
Tutti i movimenti rigidi del piano (anche uscendone) si possono ottenere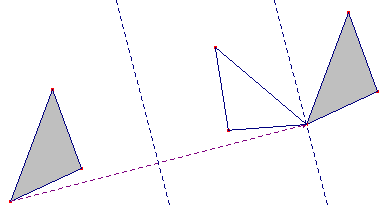 
componendo simmetrie assiali
