Summary. The author describes constructions with Cabri-géomètre vs. 1.7 to draw the parabola defined by three points and the direction of the axis, in order to get the intersections between a straight line and a parabola and the intersections between two parabolas with parallel axes. For such constructions he applies methods of projective geometry.

1.

È noto che l’ambiente Cabri-géomètre, ideato per fare geometria elementare sfruttando didatticamente la tecnologia informatica, tra i maggiori vantaggi consente di realizzare luoghi geometrici servendosi dell’opzione Luogo di Punti del menu Costruzioni Per tracciare coniche è possibile fare ricorso a molti tipi di costruzioni particolari oppure a metodi assai generali come quelli proiettivi, basati cioè esclusivamente su aspetti grafici anziché metrici, per costruire ad esempio la conica passante per cinque punti assegnati. Tuttavia, quel che si ottiene non è mai un oggetto della geometria elementare, come lo sono una retta o una circonferenza; in Cabri non è addirittura possibile far altre operazioni se non si è prima cancellato il luogo in atto; in particolare non è possibile costruire i punti intersezione tra la conica visualizzata e una retta.

Nella sua nuova versione, Cabri II fornisce la possibilità predefinita di creare, oggetto al pari degli altri, la conica per cinque punti e consente quindi ad esempio di costruire i punti intersezione tra una conica e una retta oppure tra due coniche. Quest’ultima potenzialità, di determinare le intersezioni tra due coniche, di risolvere cioè un problema di IV grado, rende la geometria con Cabri II più potente di quella tradizionale basata su riga e compasso.

Nel seguito si mostra come risolvere con la versione 1.7 di Cabri il problema delle intersezioni conica-retta o conica-conica quando si riduce a un problema di II grado, ad esempio nel caso particolarmente interessante in cui la conica è una parabola individuata dalla direzione dell’asse e da tre suoi punti, problema comunemente affrontato e risolto per via analitica quando si approfondiscono i metodi della geometria cartesiana.

È utile innanzitutto adeguare il metodo proiettivo derivato dal teorema di Steiner allo scopo di costruire appunto la parabola passante per tre punti dati e nota la direzione dell'asse di simmetria. Tale direzione indica altri due punti della parabola, coincidenti e posti all'infinito; infatti le parabole sono coniche tangenti alla retta all’infinito.

In pratica, creati sul foglio Cabri come elementi base i punti A, B e C della parabola e una retta r parallela al suo asse di simmetria, si potrà procedere nel modo seguente:

Al variare del punto K sulla retta AB, il punto P descrive la parabola passante per A, B e C e con asse parallelo alla retta r.

Si può realizzare una costruzione di soli 13 oggetti considerando variabile la retta r e costruendo il punto K come intersezione tra r e la retta AB. Selezionata l’opzione Luogo di Punti del menu Costruzioni, indicato il punto P, afferrando e traslando la retta r, anche in questo caso viene tracciata la parabola.

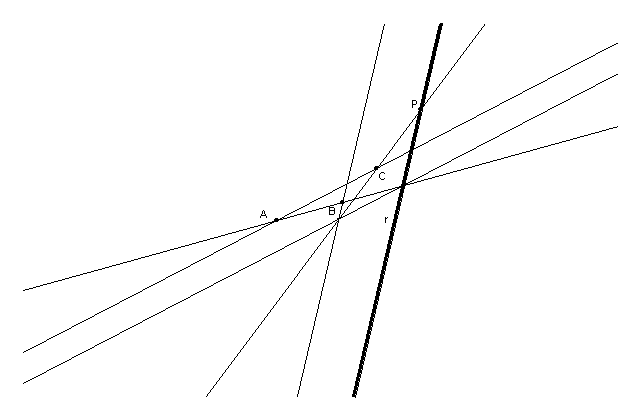
Questa può anche esser letta come costruzione dell’intersezione tra una retta e la parabola passante per tre punti e di asse parallelo a quella retta. Sarà inoltre utile per il seguito realizzarne una macro.

2.

Il problema generale di costruire le intersezioni tra una conica e una retta è di II grado, ovvero risolvibile con costruzioni riga-compasso. Per risolverlo si può dire, brevemente, che una conica induce su una retta una corrispondenza i cui punti uniti sono le intersezioni cercate.

Qui nel seguito si adatta quel metodo allo scopo di costruire le eventuali intersezioni tra una retta r e la parabola individuata da tre suoi punti A, B e C e da una retta a che indica la direzione dell’asse di simmetria.

Preliminarmente si trova la corrispondenza, una proiettività, indotta dalla parabola sulla retta. Essa si ottiene proiettando sulla retta r da due punti della parabola, per esempio da A e da uno dei suoi punti all’infinito, gli altri punti della parabola. Indichiamo dunque con X , Y e Z i punti di r tali che AX è parallelo alla retta a, Y sta sulla retta AB, Z sta sulla retta AC; analogamente X’ sarà il punto all’infinito della retta r, Y’ e Z’ i punti della retta r tali che BY’ e CZ’ sono paralleli alla retta a. Per brevità ometteremo nel seguito la descrizione dettagliata dei passi della costruzione Cabri.

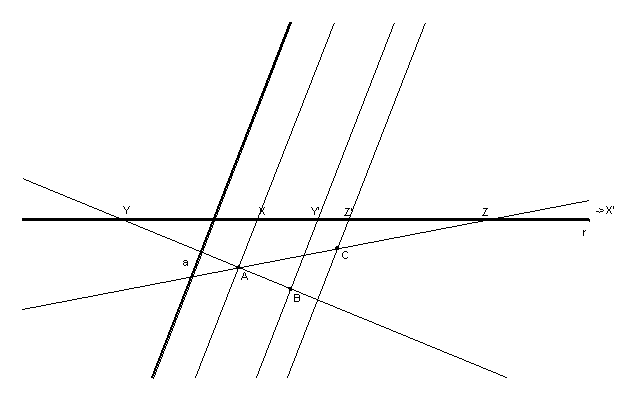
Infine si costruiscono sulla retta r i punti uniti della proiettività così indotta, punti che risolvono il problema di intersezione posto. Per questa costruzione occorre basarsi sul teorema di Staudt: una proiettività induce su una conica, in particolare su una circonferenza, una proiettività, i cui punti uniti corrispondono a quelli della retta.

Così, creata ad esempio la circonferenza di centro C e passante per A si proiettano da A i punti X, Y, Z e X’,Y’,Z’ sulla circonferenza per ottenere rispettivamente i punti X₁, Y₁, Z₁, X’₁, Y’₁, Z’₁.

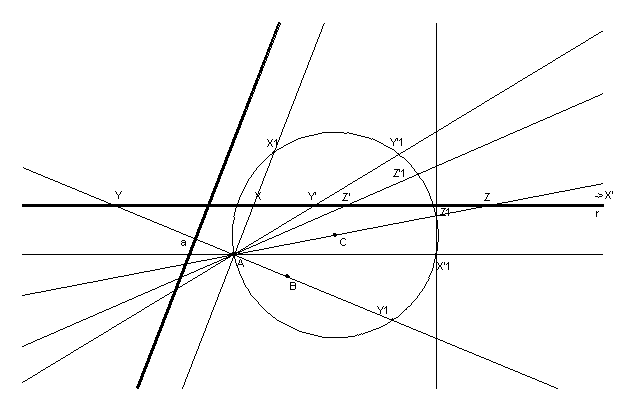
A loro volta i punti X₁, Y₁, Z₁, X’₁, Y’₁, Z’₁ si corrispondono sulla circonferenza in una proiettività che ha per punti uniti le intersezioni con la retta che passa per il punto X₁Y’_1Ç X’₁Y₁ e per il punto Y₁Z’_1Ç Y’₁Z₁.

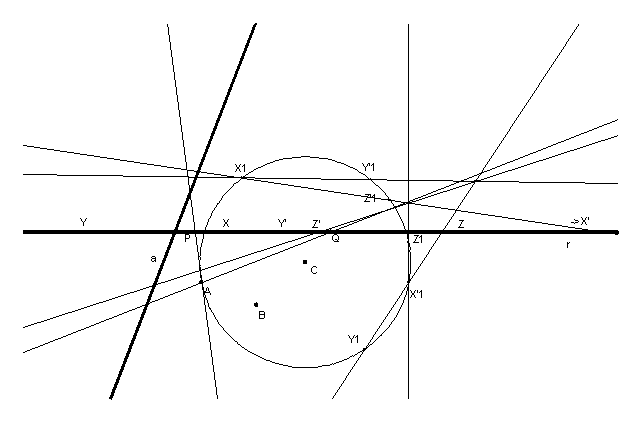
I punti uniti P e Q sulla retta, intersezioni con la parabola, si ottengono proiettando da A i punti uniti costruiti sulla circonferenza. Una tale costruzione consta di 38 oggetti.

Naturalmente con l’opzione Luogo di Punti del menu Costruzioni si può visualizzare il luogo dei punti P e Q al variare della retta, cioè la parabola data. Provare per credere! Per convincersi fino in fondo del risultato occorre approfondire tali argomenti di geometria proiettiva, una incredibile fonte di problemi e idee interessanti.

Sarà opportuno realizzare anche per questa costruzione una macro che dati i tre punti della parabola, la retta che indica la direzione del suo asse e una qualunque altra retta, costruisce le intersezioni tra parabola e retta.

3.

Anche il problema di costruire le intersezioni tra due coniche è risolvibile con riga e compasso nel caso in cui si conoscano già due punti intersezione oppure si conosca un punto di tangenza; anch’esso è descritto nella letteratura. La costruzione delle intersezioni tra due coniche tangenti in uno stesso punto a una retta data, inoltre definite ciascuna mediante altri tre punti, può essere articolata in tre fasi: individuare la corrispondenza che si ha proiettando, dal punto comune, i punti della prima conica sull’altra; trovare l’asse dei punti uniti di questa particolare corrispondenza; intersecare infine quest’asse con una delle due coniche.

Per la prima fase, poiché il punto di tangenza tra le due parabole si trova all’infinito nella direzione indicata da r, servendosi della macro realizzata precedentemente non è difficile costruire le intersezioni X’, Y’ e Z’ tra le tre rette parallele ad r condotte rispettivamente da X, Y e Z e la parabola passante per i tre punti A, B e C.

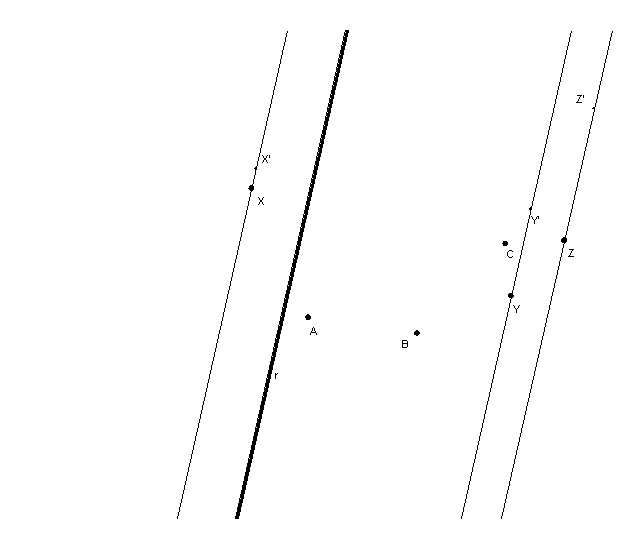
Per trovare l’asse dei punti uniti della corrispondenza, un’omologia che ha centro nel punto all’infinito e nella quale si corrispondono X e X’, Y e Y’, Z e Z’, basterà creare la retta che passa per i punti intersezioni XYÇ X’Y’ e XZÇ X’Z’.

Infine, servendosi ancora della macrocostruzione definita precedentemente, si possono costruire i punti P e Q intersezione tra le due parabole come intersezione tra la retta costruita nella seconda fase con una della due parabole.

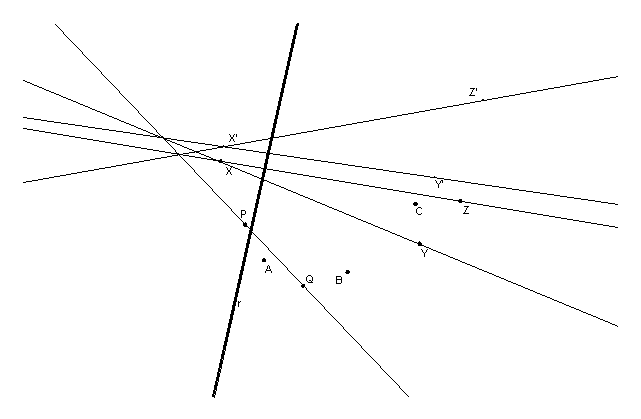
Per una tale costruzione è possibile fare ricorso solo a 70 oggetti.

Scimemi B., Pappo, Pascal, Steiner e la generazione proiettiva delle coniche, CABRIIRSAE n°3, Bologna '94.

Enriques F., Lezioni di geometria proiettiva, Zanichelli, Bologna 1996.