
<< pagina principale < ······················ << articoli < ······················
Roberto Ricci L.S. "A.Righi", Bologna
Introduzione
L'informatica può favorire un approccio sperimentale alla matematica, e in tal caso il laboratorio d'informatica diventa laboratorio di matematica. Un foglio elettronico si o qui usato il LOTUS 123 - è un ambiente che offre buone prestazioni in rapporto alle conoscenze tecnico-programmative indispensabili. Mostreremo come in tale ambiente sia possibile rappresentare semplici figure geometriche e, soprattutto, come si possano osservare dinamicamente per sperimentarne alcune proprietà. Si tratta di esperienze proponibili in un biennio di scuola secondaria superiore, sia allo scopo d'introdurre all'uso del foglio elettronico e alle sue funzionalità grafiche sia per fornire allo studente stimoli di riflessione su semplici questioni di geometria sintetica. Gli esempi che seguono non sono dunque più di semplici esercizi, sia di informatica che di matematica. Occorre aggiungere che esistono ambienti pio specificatamente attrezzati per uno studio sperimentale della geometria sintetica nel piano, come ad esempio Cabri-géomètre; un'alternativa a carta, matita, gomma righello e compasso per la costruzione di figure geometriche e per l'esplorazione delle loro proprietà.
Baricentro
Realizzare un F.E. per disegnare triangoli è semplice. Sari sufficiente sistemare su due colonne le coordinate dei tre vertici, ripetendo in ultimo quelle del primo punto per chiudere la spezzata con cui verranno congiunti i vertici:
| A | B | C | D | E | |
| 1 | |||||
| 2 | |||||
| 3 | 60 | 30 | |||
| 4 | 50 | 10 | |||
| 5 | 5 | 40 | |||
| 6 | 80 | 30 |
come mostra l'elenco delle formule associate alle celle;
B3: 80 C3: 30 B4: 50 C4: 10 B5: 5 C5: 40 B6: +B3 C6: +C3
Per realizzare il grafico sarà sufficiente selezionare il tipo XY, associare la prima colonna all'asse X e la seconda ad A, eventualmente fissare manualmente i limiti inferiore e superiore di ogni asse nonché variare la scala per rendere monometrico il sistema.

Nel foglio si possono anche aggiungere le mediane:
| A | B | C | D | E | |
| 1 | |||||
| 2 | |||||
| 3 | 60 | 30 | |||
| 4 | 50 | 10 | |||
| 5 | 5 | 40 | |||
| 6 | 80 | 30 | |||
| 7 | |||||
| 8 | 80 | 30 | |||
| 9 | 27,5 | 25 | |||
| 10 | |||||
| 11 | 50 | 10 | |||
| 12 | 42,5 | 35 | |||
| 13 | |||||
| 14 | 5 | 40 | |||
| 15 | 65 | 20 |
in cui punti le cui coordinate sono separate da una riga vuota non verranno graficamente congiunti tra loro.
Le formule sono:
B8: +B3 C8: +C3 B9: (B4+B5)/2 C9: (C4+C5)/2 B11: +B4 C11: +C4 B12: (B5+B6)/2 C12: (C5+C6)/2 B14: +B5 C14: +C5 B15: (B4+B3)/2 C15: (C4+C3)/2
e quindi il grafico
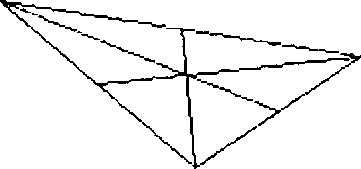
Variando le coordinate dei vertici del triangolo si può osservare che le mediane s'intersecano sempre in uno stesso punto, detto baricentro.
Una generalizzazione
Anziché considerare i segmenti congiungenti i vertici del triangolo con il punto medio del lato opposto si può pensare di attribuire a ciascun vertice un peso, eventualmente anche negativo, e congiungere ogni vertice con il "baricentro" del lato opposto; ovvero, detti pA e pB ad esempio i pesi dei vertici A e B, il "baricentro" del segmento AB sarà quel punto P della retta AB tale che
AP/PB = pB/pA
coincidente con il punto medio solo se pA= pb.
II foglio potrà apparire come nel seguito:
| A | B | C | D | E | F | |
| 20 | 35 | 25 | pA = | 1 | ||
| 21 | 25 | 20 | pB = | -2 | ||
| 22 | 20 | 35 | pC = | 1 | ||
| 23 | 35 | 25 | ||||
| 24 | ||||||
| 25 | 35 | 25 | ||||
| 26 | 30 | 5 | ||||
| 27 | ||||||
| 28 | 25 | 20 | ||||
| 29 | 27, 5 | 30 | ||||
| 30 | ||||||
| 31 | 20 | 35 | ||||
| 32 | 15 | 15 |
con le formule seguenti:
B20: 35
C20: 25
E20: "pA =
F20: 1
B21: 25
C21: 20
E21: "pB =
F21: -2
B22: 20
C22; 35
E22: "pC =
F22: 1
B23: +B20
C23: +C20
B25: +B20
C25; +C20
B26: ($F$21*B21+$F$22*B22)/($F$21+$F$22)
C26: ($F$21*C21+$F$22*C22)/($F$21+$F$22)
B28: +B21
C28: +C21
B29: ($F$22*B22+$F$20*B20)/($F$22+$F$20)
C29: ($F$22*C22+$F$20*C20)/{$F$22+$F$20)
B31: +B22
C31: +C22
B32: ($F$20*B20 + $F$21*B21)/($F*20+$F$21)
C32: ($F$20*C20 + $F$2i*C21)/($F$20+$F$21)
Si può osservare ancora, sia variando le coordinate dei vertici del triangolo, sia variando i pesi, che tali gmenti, eventualmente prolungati, s'intersecano in uno esso punto
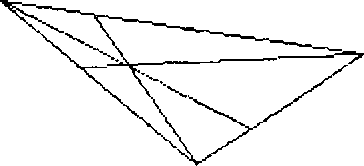
Dimostrarlo non è difficile: detti
PA = (pB*B + pC*C)/(pB + pC), PB = (pA*A + pC*C)/(pA + pC)
PC> = (pA*A + pB*B)/(pA + pB), P = (pA*A +pB*B + pC*C)/(pA + pB + pC)
si osservi che
P =(PA *A+(pB + pC)*P A )/(p A +(pB + p C ) ), quindi P sta su AP A
P =(PB*B+(p A + p C )*P B )/(p B +(p A + p C ) ), quindi P sta su BP B
P =(PC *C+(pA + p B )*P C )/(p C +(p A + p B ) ), quindi P sta su CP C;
Incentro
Quali eventuali pesi attribuire ai vertici per ottenere l'incentro, cioè il punto d'incontro delle bisettrici? Si può constatare che ciò si ottiene semplicemente pesando ciascun vertice con la lunghezza del lato opposto. Ecco dunque il foglio per rappresentare le bisettrici di un triangolo:
| A | B | C | D | E | F | |
| 41 | 80 | 30 | a = | 62,64982 | ||
| 42 | 60 | 10 | b = | 75,66372 | ||
| 43 | 5 | 35 | c = | 28,28427 | ||
| 44 | 80 | 25 | ||||
| 45 | ||||||
| 46 | 80 | 30 | ||||
| 47 | 45,03448 | 18,16300 | ||||
| 48 | ||||||
| 49 | 60 | 100 | ||||
| 50 | 56,67189 | 33,11041 | ||||
| 51 | ||||||
| 52 | 5 | 40 | ||||
| 53 | 69,05910 | 19,05910 |
essendo le formule:
B41: 60
C41: 30
E41: "a =
F41: @RADQ((B42-B43)^2+ (C42-C43 )^2)
B42: 60
C42: 10
E42: " b =
F42: @RADQ((B41-B43)^2 + {C41-C43)^2)
B43: 5
C43: 40
E43: "C =
F43: @RADQ((B41-B42)^2 + (C41-C42)^2)
B44: +B41
C44: +C41
B46: +B41
C46: +C41
B47: ($F$42*B42 + $F$43*B43 )/($F$42 + $F$43)
C47: ($F$42*C42 + $F$43*C43 )/($F$42 + $F$43)
B49: +B42
C49: +C42
B50: ($F$43*B43 + $F$41*B44)/($F$43 + $F$41)
C50: ($F$43*C43 + $F$41*C44)/($F$43 + $F$41)
B52: +B43
C52: +C43
B53: ($F$41*B41 + $F$42*B42)/($F$41 + $F$42)
C53: ($F$41*C41 + $F$42*C42)/($F$41 + $F$42)
Ad esempio si può vedere la figura seguente
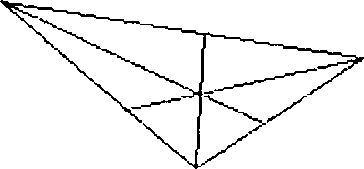
Si può anche dimostrare facilmente che
appunto, nel caso CPC
sia bisettrice, detta D la sua intersezione con la parallela per
A al lato CB, osservato che DAC è isoscele e che i triangoli APCD
e BPCC
sono simili, allora APC/PCB
= b/a .
Ortocentro
Quali pesi attribuire invece ai vertici per ottenere l'ortocentro, cioè il punto d'incontro delle altezze? Si deve pensare al teorema di Pitagora: A è retto se e solo se b 2 + c 2 - a 2 =0, e in tal caso P A deve coincidere con A stesso; ciò può suggerire di pesare ciascun vertice con il reciproco di b 2 + c 2 - a 2 , realizzando quindi un foglio come il seguente:
| A | B | C | D | E | F | |
| 62 | 55 | 30 | pA = | 0,0005 | ||
| 42 | 25 | 10 | pB = | -0,00666 | ||
| 43 | 20 | 35 | pC = | 0,001538 | ||
| 44 | 55 | 25 | ||||
| 45 | ||||||
| 46 | 55 | 25 | a = | 15,81138 | ||
| 47 | 26,5 | 15,5 | b = | 36,40054 | ||
| 48 | c = | 30,41381 | ||||
| 49 | 25 | 20 | ||||
| 50 | 28,58490 | 32, 547 | ||||
| 51 | ||||||
| 52 | 20 | 35 | ||||
| 53 | 22, 56756 | 19, 59459 |
in cui le formule sono:
B62: 55 C62: 25 E62: "pA = F62: 1/(F68^2 + F69^2 - F67^2) B63: 25 C63: 20 E63: "pB = F63: 1/(F67^2 + F69^2 - F68^2) B64: 20 C64: 35 E64: "pC = F64: 1/(F67^2 + F68^2 - F69^2) B65: +B62 C65: +C62 B67: +B62 C67: +C62 E67: "a = F67: @RADQ((B63-B64)^2+ (C63-C64)^2) B68: ($F$63*B63+$F$64*B64)/($F$63+$F$64) C68; ($F$63*C63+$F$64*C64)/($F$63+$F$64) E68: "b = F68: @RADQ((B62-B64)^2+ (C62-C64)^2) E69: "c = F69: @RADQ((B62-B63)^2+ (C62-C63)^2) B70: +B63 C70: +C63 B71: ($F$64*B64+$F$62*B65)/($F$64+$F$62) C71: ($F$64*C64+$F$62*C65)/($F$64+$F$62) B73: +B64 C73: +C64 B74: ($F$62*B62+$F$63*B63)/($F$62+$F$63) C74: ($F$62*C62+$F$63*C63)/($F$62+$F$63)
Che in tal modo si ottengano veramente le altezze lo si pud mostrare semplicemente ad esempio con la trigonometria:
AH/HB = b*cos&alfa;/a*cosβ =
((b 2 + c 2 - a 2 )/(2c))/((a 2 + c 2 - b 2 )/(2c)) =
= (b 2 + c 2 - a 2 )/(a 2 + c 2 - b 2 ).
Ci si può convincere anche osservando grafici come quelli delle figure seguenti.
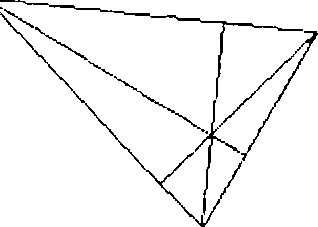 |
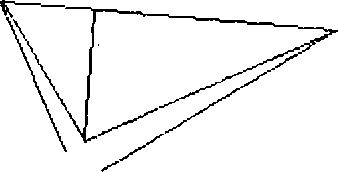 |
Bibliografia
Projet <<Cabri - gèomètre>>, Laboratoire de Structures Discrètes et de Didactique, Tour Irma BP 53X, 380412 Grenoble cedex.
LOTUS Dev, Corp. : 123, Manuale di consultazione.
AA.VV.: L'elaboratore nella formazione e nella didattica, Pitagora, Bologna 1990.