Il moto dei proiettili
Roberto Ricci
L.S. "A. Righi"- Bologna
L'analisi del moto del proiettile è argomento di cinematica tra i più significativi affrontati nel corso del terzo anno di un liceo scientifico. Se si trascura l'attrito viscoso con l'aria, tale analisi si basa sul principio di composizione dei movimenti e richiede conoscenze dei moti uniformi e uniformemente vari nonché di geometria cartesiana per determinare la traiettoria parabolica.
Analisi assai dettagliate di questo moto furono svolte da Galileo Galilei con gli strumenti concettuali allora a disposizioni: ancora sostanzialmente di geometria sintetica per la matematica, poi quelli che egli stesso andava sviluppando per la nascita della scienza della fisica modernamente intesa. Tali studi, che non erano soltanto speculativi, produssero un risultato di un certo rilievo con la costruzione di un compasso militare, rielaborato anche dall'allievo Evangelista Torricelli.
Il compasso, detto anche squadra militare, poteva essere usato come squadra per stabilire l'alzata delle bombarde ed è descritto in: Le operazioni del Compasso geometrico et militare di GALILEO GALILEI, Nobil Fiorentino, Lettore delle Matematiche nello studio di Padova, 1606.

Nel sito Internet http://galileo.difi.unipi.it/sezdid/antologia/opere/ presso l'università di Pisa si possono trovare immagine del frontespizio dell'opera e altre informazioni come la seguente:
Famoso il plagio del milanese Baldassare Capra, che tradusse l'opera in latino spacciandola per sua, ma accusato da Galileo, fu condannato dai Riformatori dell'Università di Padova a distruggere le copie del libro, e la sentenza fu bandita a suon di tromba. In quell'occasione, a difesa del proprio buon diritto, Galileo scrisse:
Difesa di GALILEO GALILEI, Nobile Fiorentino, Lettore delle Matematiche nello studi o di Padova, contro alle calunnie ed imposture di Baldassar Capra milanese. Usategli sì nella Considerazione Astronomica sopra la Nuova Stella del MDCIII come (et assai più) nel publicare nuovamente come sua invenzione la fabrica, et gli usi del Compasso Geometrico, et Militare, sotto il titolo di Usus et fabrica Circini cuiusdam proportionis, etc. In Venetia, 1607, presso Tomaso Baglioni.
Nell'Edizione nazionale delle Opere di GALILEO GALILEI, il Compasso è pubblicato nel volume Il, pp. 363-424, la Difesa nello stesso volume, pp. 513-601.
Con una semplice costruzione si può illustrare l'idea di base della squadra militare di Galileo (si veda ad es. M.E. Bergamaschini, P.Marazzini, L.Mazzoni, Fisica 1, Carlo Signorelli, Milano, 1996).
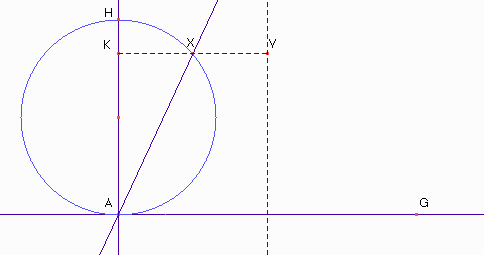
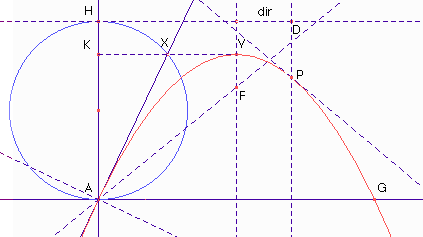
Il diametro AH della circonferenza, elemento fondamentale della costruzione, ha lunghezza pari all'altezza che il proiettile raggiungerebbe se fosse sparato verticalmente, cioè v2/(2g) se v è la velocità impressa al proiettile e g l'accelerazione di gravità. L'inclinazione della retta AX rappresenta l'alzata del mortaio e quindi AK ha lunghezza vy2/(2g) se vy è, in questo caso, la componente verticale della velocità. Dati la velocità del proiettile e l'alzata del mortaio la costruzione permette di determinare in particolare la gittata.
Il punto V di massima quota raggiunto dal proiettile è costruito come simmetrico di K rispetto a X; il punto G, gittata del mortaio, è costruito come simmetrico di A rispetto alla verticale per V. Dunque la gittata è quattro volte la lunghezza KX. D'altra parte
KX2 = AK× KH = ( v2/(2g) - vy2/(2g) ) × vy2/(2g) = ( vx2/(2g) ) × vy2/(2g)
se vy è la componente orizzontale della velocità; allora KX ha lunghezza vxvy/(2g) e quindi la massima distanza orizzontale percorsa dal proiettile è 2vxvy/g.
Possiamo anche costruire la traiettoria parabolica del proiettile individuando il fuoco F come intersezione tra l'asse di simmetria della parabola, la verticale per V, e la retta simmetrica di AH rispetto alla perpendicolare da A ad AX, tangente alla traiettoria. Infatti una delle proprietà più note della parabola è che raggi paralleli all'asse di simmetria della parabola, come AH, vengono riflessi dalla curva in modo da passare per il fuoco. La direttrice, inoltre, è la retta perpendicolare all'asse della parabola passante per il punto simmetrico del fuoco F rispetto al vertice V. Si noti che la direttrice passa per il punto H .
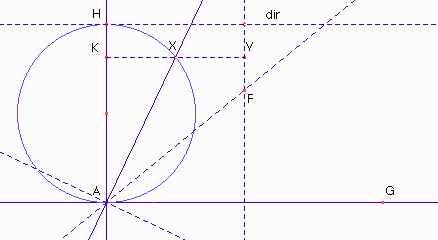
La traiettoria parabolica si può ottenere poi con la solita costruzione: preso un punto D sulla direttrice, costruito il punto P intersezione dell'asse di FD e della perpendicolare da D alla direttrice, si costruisce il luogo dei punti P al variare di D.