Roberto Ricci
Liceo Scientifico "A.Righi"- Bologna
Per una lettura corretta del testo occorre avere installato i font di caratteri TI-92 symbols e TI92PC
Metodo delle approssimazioni successive
Tradizionalmente, per l'apprendimento dei saper fare matematica, lo studente è generalmente messo di fronte a esercizi concepiti appositamente per l'impiego di metodi di risoluzione esatta. Si tratta quindi per lo più di situazioni artificiose, come in una palestra attrezzata per sviluppare solo ben determinati muscoli. Sappiamo tuttavia che, nell'infinita casistica di situazioni problematiche in ambito matematico, accade spesso di non poter far uso quei metodi.
Quando non si conoscono metodi esatti per risolvere un'equazione è generalmente inevitabile ricorrere al metodo delle approssimazioni successive.
Nell'era iniziata con la rivoluzione dell'automazione elettronica dei processi di calcolo numerico, questo metodo si è subito imposto in modo del tutto naturale perché emblematico del modo di pensare algoritmico e perché è alla base della successiva evoluzione dei metodi di calcolo numerico. Era tuttavia già conosciuto e applicato dai Babilonesi per calcolare radici quadrate - metodo talvolta attribuito al greco Archita (426-435 a.c.) o ad Erone d'Alessandria ( vissuto tra I e II sec d.c.) -; è noto come metodo della falsa posizione presso gli egiziani; è possibile riconoscerlo inoltre nelle argomentazioni prodotte da Zenone d'Elea nel 500 a.c. circa. Fu successivamente reintrodotto da Isaac Newton nel Metodo delle flussioni e nel De Analisi appunto per il calcolo approssimato delle soluzioni delle equazioni: applicato al caso particolare delle radici quadrate si riduce al metodo dei babilonesi.
In effetti uno dei primi problemi che si pongono nell'insegnamento/apprendimento della matematica è quello della distinzione espressioni per rappresentare numeri irrazionali, non rappresentabili in modo esatto con numeri in forma decimale limitata, ed espressioni decimali esatte per rappresentare risultati di un loro calcolo approssimato, ottenuto spesso in modo nascosto attraverso una calcolatrice; questo accade ad esempio quando, da soluzioni esatte delle equazioni di secondo grado attraverso la nota formula, si passa a una loro valutazione numerica approssimata.
Se anche le più modeste calcolatrici tascabili estraggono radici mentre le più sofisticate risolvono equazioni senza che l'utente se dia pena di sapere come, l'insegnante ha il dovere di ricordare che queste macchine implementano algoritmi di calcolo approssimato, e dove possibile è importante che esamini i metodi fondamentali, quelli che hanno preceduto gli algoritmi oggi più efficienti, tra gli oggetti di studio dell'analisi numerica.
Si tratta inoltre di un tipico argomento di integrazione tra matematica e informatica - da affrontare non necessariamente dopo il calcolo infinitesimale ma, in parte, anche prima per motivare al concetto di limite - che può stimolare l'uso del laboratorio servendosi sia di linguaggi di programmazione tradizionali sia di altri ambienti come il foglio elettronico.
Nel seguito si suggerisce l'uso della calcolatrice grafica TI-92 per rendere più disinvolta un'esposizione pratica di questi metodi dal momento che offre un ambiente integrato che unisce un manipolatore simbolico per il calcolo della funzione derivata a quello di programmazione in un linguaggio stile Pascal.
Il metodo delle approssimazioni successive (o iterativo) si applica alla risoluzione di un'equazione f(x)=0 dopo averla trasformata in una ad essa equivalente del tipo x=g(x).
Diversi sono i metodi per realizzare questa trasformazione, anche perché non qualsiasi funzione g(x) è opportuna per poter applicare con successo - nonché efficientemente - quello delle approssimazioni successive: occorre che a partire da un valore iniziale x1 , la successione
xn=g (xn-1)
sia convergente. Quando ciò accade questo limite è una soluzione dell'equazione data. Infatti dalle premesse:
i) ![]() , e dunque,
poiché g(xn)= xn+1 , anche
, e dunque,
poiché g(xn)= xn+1 , anche ![]()
ii) g è continua, e dunque ![]()
consegue, per l'unicità del limite, che x = g(x).
Per esemplificare concretamente il metodo iniziamo per semplicità dalla ricerca delle soluzioni della seguente equazione: x= cos(x).
Con la calcolatrice TI-92 è possibile reiterare il calcolo in ambiente " sulla base della funzione ± che fornisce il risultato del precedente calcolo. Ciò semplicemente digitando in ambiente " :
1
cos(± (1))
e ripetere quest'ultimo calcolo.
Dopo aver definito per comodità la funzione g(x) con la calcolatrice
cos(x) § g(x)
è anche possibile definire una sequenza
1 § ui1
g(u1(n-1)) § u1(n)
e valutare ad esempio il 20° elemento della successione delle approssimazioni
u1(20)
o visualizzarne l'andamento con la modalità GRAPH ….SEQUENCE.
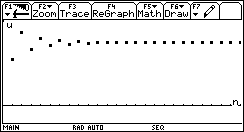
Per dare anche un'immagine grafica del metodo delle approssimazioni successive si può sfruttare la possibilità offerta dalla calcolatrice grafica TI-92 dei grafici a ragnatela selezionando in ambiente # l'opzione ‰ Axes: WEB.

Per valutare l'importanza della scelta di g(x) consideriamo ora un'equazione come quella per trisecare l'angolo: posto x=cos(a/3), dalle formule di triplicazione cos(3·a ) = 4 cos3a - 3cosa , dovrà essere 4 x3 - 3x - cosa = 0.
Se trasformiamo l'equazione in modo da porre: g(x) = (4 x3 - cosa )/3,
(4 x3 - 1/2 )/3 § g(x)
1
g(± (1))
si può vedere che la sequenza diverge a -¥ , anche in modalità GRAPH ….SEQUENCE
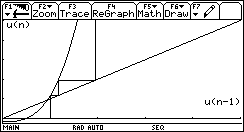
Si verifica che conviene considerare piuttosto la seguente
forma equivalente: ![]() . Con la calcolatrice
. Con la calcolatrice
((3 x + 1/2 )/4)^(1/3) § g(x)
1
g(± (1))
la sequenza converge velocemente a .939692… e 3 cos-1(.939692…) = 1.047197… = p /3.
Nell'immagine seguente si è preso come approssimazione iniziale 0.2 per rallentare e così visualizzare meglio il processo di convergenza.
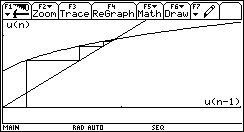
Per evitare di effettuare manualmente il calcolo di ogni primo elemento della successione approssimante, che è ricorsivo in avanti, si può definire una funzione, ancora ricorsiva ma all'indietro, come la seguente:
when(n>1,iteraN(g(x),n- 1),g(x)) § iteraN(x,n)
Per calcolare ad esempio il 10° elemento della successione approssimante dello zero della precedente equazione:
iteraN(1,10)
Alternativamente, ponendo come passo finale della ricorsione un controllo sull'errore di approssimazione, si può considerare la funzione:
when(abs(g(x)- x)<r,g(x),itera(g(x),r)) § itera(x,r)
e calcolare il valore che approssima x a meno di 10-6
itera(1,10^6)
È opportuno sottolineare che per calcolare g(x) nei casi precedenti si danno già per scontato algoritmi di calcolo approssimato per le funzioni come cos(x) e la radice cubica, cosicché l'arrotondamento inevitabile nel calcolo dei valori di g(x) può causare, per scelte dell'approssimazione troppo piccole, delle periodicità nella successione dei valori approssimanti xn della soluzione cercata. Perciò è meglio sostituire il controllo sull'errore assoluto | xn- xn-1 | con quello sull'errore relativo | xn- xn-1 | / xn-1.
when(abs((g(x)- x)/x)<r,g(x),itera(g(x),r)) § itera(x,r)itera(1,10^3)
Ricordiamo inoltre che definizioni ricorsive come quelle proposte per le funzioni di iterazione sono, per quanto più eleganti e significative nella loro capacità di sintesi, meno efficienti di quelle basate su strutture di ripetizione; è quindi più efficiente realizzare un programma come il seguente
:Iterazi(x,appr)
:Prgm
:ClrIO
:While abs(g(x)/x-1) > appr
: approx(g(x)) § x
:EndWhile
:Disp x
:EndPrgm
Ovvero, per vedere dinamicamente la variazione dei valori approssimanti,
:Iterazi(x,appr)
:Prgm
:ClrIO
:While abs(g(x)/x-1) > appr
: approx(g(x)) § x
: Output 1,1, x
:EndWhile
:EndPrgm
Chiarita l'importanza del ruolo svolto dalla funzione g è bene passare ad analizzarne le caratteristiche che possono garantire il successo e l'efficienza del metodo delle approssimazioni successive.
Affinché l'equazione x = g(x) abbia almeno una soluzione sufficiente che
g: [a,b] ® [a,b] sia continua e g([a,b]) Í [a,b].
Infatti posto h(x) = g(x) - x si ha che h(a) ³ 0 e h(b) £ 0; dunque, essendo h continua, $ x tale che h(x) = 0, ovvero x è punto fisso per la funzione g.
Tuttavia non è detto che, a partire da un qualunque valore iniziale x1 , la successione delle iterate xn= g(xn-1) sia convergente.
Affinché xn= g(xn-1) sia convergente è sufficiente che la funzione g(x) sia una contrazione, cioè che g sia continua e che inoltre la pendenza m di una qualunque secante del suo grafico - oppure, al limite, di qualunque sua tangente - soddisfi la condizione |m| £ q < 1.
Infatti, se il valore iniziale x1 è in un intervallo [a,b] allora
x2= g(x1) Î [a1,b1]=g([a,b])=[g(a ), g(b )] con |b1 - a1| £ q·|b -a | £ q·|b-a| e in generale
xn+1= g(xn) Î [an,bn] con |bn - an| £ qn |b- a|;
poiché l'intervallo [an,bn] diventa infine di ampiezza nulla, ed è contenuto in [a,b], siamo certi che la successione degli an e dei bn, quindi la successione degli xn, convergono per la continuità di R.
Si possono anche distinguere punti intorno ai quali il processo di iterazione converge stabilmente:
se g: R ® R , g è derivabile, s =g(s) allora:
se |g'(s)| < 1 allora s è un attrattore, cioè ha un intorno per ogni punto x1 del quale la successione xn = g(xn-1) converge a s;
se |g'(s)| > 1 allora s è un repulsore, cioè ha un intorno per ogni punto x1 del quale la successione xn = g(xn-1) non converge a s ( s è dunque un attrattore per la funzione inversa g-1 ).
Per quanto riguarda la qualità e la rapidità della convergenza alla soluzione cercata x, osservato che |g(xn+1) - g(xn)| £ qn |x2- x1|, possiamo dire che
| xn- x | £ |xn- x n+1| + |xn+1- x n+2| + ….£ qn |x2- x1| + qn+1 |x2- x1| + …. = |x2- x1 | qn / (1- q)
e inoltre
| xn- x | £ |xn- x n+1| + |xn+1- x n+2| + ….£ q |xn- xn-1| + q2 |xn- xn-1| + …. = | xn- xn-1| q / (1- q) che è l'errore commesso nell'approssimazione fermandosi al valore xn.
Nel caso più semplice che la f(x) sia derivabile e f'(x) limitata sul suo dominio [a,b], possiamo sempre determinare opportunamente un valore l in modo che g(x)= l ·f(x) + x faccia al caso nostro. Infatti da m < f'(x) < M e |g'(x)|= |l ·f'(x) + 1| < max{ |l ·m + 1| , |l ·M + 1| } si vede che è possibile scegliere l in modo che max{ |l ·m + 1| , |l ·M + 1| } < 1.
Il metodo delle approssimazioni successive si può applicare
anche alla risoluzione di un sistema di equazioni ![]() dopo averlo
trasformato in uno ad essa equivalente del tipo
dopo averlo
trasformato in uno ad essa equivalente del tipo ![]() .
.
Come già detto, un esempio particolarmente significativo è quello del calcolo delle radici n-esime, soluzioni dell'equazione: xn = r.
Trasformare l'equazione in x = r/xn-1 e considerare g(x) = r/xn-1 non porta ad alcun risultato. Ad esempio volendo calcolare le radici quadrate, a partire da un qualunque primo valore x1 si ottiene infatti la successione oscillante x1, r/x1, x1, r/x1, …
Un metodo ottenuto sulla base di considerazioni euristiche nasce nell'ipotesi ottimistica di conoscere già un'approssimazione a, ponendo cioè x = a+h dove quindi h è un valore piccolo. Così, poiché xn = (a+h)n = an+nan-1h+ … + nahn-1+ hn @ an+nan-1h, l'equazione da risolvere può essere approssimata con: an+nan-1h = r.
solve(a^n+n*a^(n- 1)h=r,h)a+right(ans(1)) § radapp(n,r,a)
Si ottiene che radapp(n,r,a) equivale a (r+(n- 1)an)/(n·an-1).
Dunque per calcolare con questo metodo un'approssimazione della radice cubica di 5:
5
radapp(3,5,ans(1))
Si verifica facilmente che posto g(x) = (r+(n- 1)xn)/(n·xn-1), l'equazione x = g(x) equivale all'equazione da risolvere xn = r.
Ci si può chiedere a questo punto se la funzione da iterare g(x) è una contrazione.
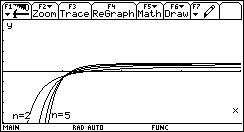
Si può visualizzare i grafici di g(x) per alcuni valori di n e per r=2 e le corrispondenti funzioni derivate g'(x).
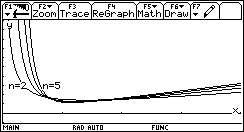
Poiché (g(x2)- g(x1))/(x2- x1) = (n- 1)/n + r (x2-n - x1-n)/n ovvero g'(x) = (1 - r/xn) (n - 1)/n non si può dire - anche guardando i grafici in particolare dove xn< r - sia sempre una contrazione.
Questo metodo può essere visto come applicazione di un metodo più generale, il metodo delle tangenti di Newton, o di Newton-Raphson. Esso consiste nel sostituire alla curva grafico di y=f(x) in un punto di ascissa a, considerato una prima approssimazione dello zero, la retta tangente di equazione y = f(a) + f'(a)·(x- a); quindi consiste nell'approssimare f(x) = 0 con l'equazione
f(a) + f'(a)·(x- a) = 0
per cercare una nuova migliore approssimazione x = a- f(a)/f'(a).
Si verifica facilmente che nel caso di f(x) = xn - r allora a- f(a)/f'(a) = (r+(n- 1)an)/(n·an-1).
Con la calcolatrice possiamo procedere come nel seguito:
x-cos(x) § f(x)zeros(f(a)+(x- a)*(D(f(x),x)|x=a),x)[1] § ztang(a)
1ztang(ans(1))
Possiamo costruire un'immagine grafica del metodo.
In ambiente # e 3 graph: FUNCTION possiamo infatti definire
y1 = f(x)
y2 = f(xo) + m(x- xo)
avendo precedentemente calcolato in ambiente " le liste xo ed m che hanno per elementi rispettivamente i diversi valori che approssimano lo zero cercato e le pendenze delle rispettive tangenti:
dopo aver selezionato 3 graph : SEQUENCE
seq(u1(n), n, 0, 5) § xo
seq(d(f(x),x) | x=u1(n), n, 0, 5) § m
Nel seguito è mostrato il risultato grafico per le prime due iterazioni a partire dal valore iniziale 3:
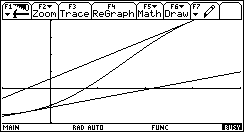
Ecco il terzo passo e infine altre tre fasi dell'iterazione
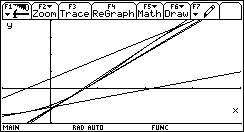
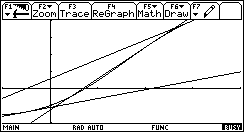
Si verifica subito che posto g(x) = x- f(x)/f'(x) l'equazione x=g(x) equivale a f(x)=0.
Dunque, constatato che il metodo delle tangenti è un metodo generale per costruire la solita funzione da iterare g(x), vale la pena di chiedersi se questa g(x) è una contrazione.
Si ha che g'(x) = f(x)f"(x)/(f'(x))2. Anche in questo caso g(x) non è una contrazione e c'è convergenza solo quando l'approssimazione iniziale è abbastanza vicina alla soluzione cercata.
Ancora più in generale si può considerare lo sviluppo in serie di Taylor di g(x) ad esempio fino al secondo grado:
zeros(taylor(f(x),x,2,a),x)[ 2] § ztaylor(a)
Ma si può anche rinunciare a quello delle tangenti accontentandosi di ricorrere a un analogo metodo delle secanti, che non necessita della conoscenza del concetto di derivata.
zeros(f(a)+(x- a)*(f(b)- f(a))/(b- a),x)[1] § zsec(a,b)
zsec(1,2)
zsec(1,ans(1))
Vediamo il significato geometrico nel caso a=3 e inizialmente b = - 1, mostrando le prime due iterazioni
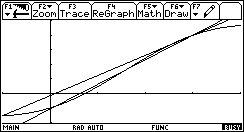
E quindi altre tre fasi successive del processo
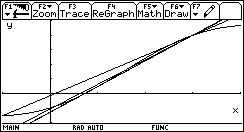
Facile anche in questo caso verificare che x= x- f(x)(x- a)/(f(x)- f(a)) equivale a f(x)=0.
Quindi posto g(x) = x- f(x)(x- a)/(f(x)- f(a)) ricadiamo ancora nel metodo descritto sin dall'inizio anche se non è sempre possibile verificare che g(x) sia una contrazione.
Infine il più semplice metodo che fa uso di approssimazioni successive per il calcolo degli zeri di una funzione è il metodo di bisezione o di Bernard Bolzano (1781-1848). Individuato un intervallo [a,b] ai cui estremi la funzione ha valori discordi di segno, ad esempio [-1/2 , 2], il metodo può essere descritta nel modo seguente:
-1/2
2
when(f(ans(1))*f(ans(2)<0, (ans(1)+ans(2))/2)
when(f(ans(1))*f(ans(2)<0, (ans(1)+ans(2))/2, (ans(1)+ans(3))/2)
when(f(ans(1))*f(ans(2)<0, (ans(1)+ans(2))/2, (ans(1)+ans(3))/2)
…
L'errore compiuto è | xn- x | £ (b- a)/2n+1.
Questo metodo può essere variato leggermente considerando, anziché il punto di mezzo, il centro di massa del segmento [a,b] pesando gli estremi con |f(b)| e |f(a)|; si ottiene il più antico metodo della falsa posizione:
-1/2
2
when(f(ans(1))*f(ans(2)<0, (ans(1)*f(ans(1))-ans(2)*f(ans(2)))/ (f(ans(1))-f(ans(2))))
when(f(ans(1))*f(ans(2)<0, (ans(1)*f(ans(1))-ans(2)*f(ans(2)))/ (f(ans(1))-f(ans(2))), (ans(1)*f(ans(1)-ans(3)*f(ans(3)))/ (f(ans(1))-f(ans(3))))
…
Anche in questi casi il metodo, seppure in modo meno evidente, si appoggia a una opportuna scelta generale della funzione g(x) da iterare secondo il metodo comune delle approssimazioni successive.
Pur non essendo basati su contrazioni, i metodi prima descritti convergono con una certa rapidità se si sceglie come approssimazione iniziale un valore non distante dalla approssimazione cercata. Si pone così il problema della rapidità di convergenza. Il metodo delle tangenti è generalmente più rapido di quello delle secanti che a sua volta è generalmente più rapido di quello di bisezione.
Per quanto riguarda la velocità di convergenza si può distinguere almeno in due casi:
| xn+1- x | / | xn- x | = | g(xn)- g(x) | / | xn- x | = g'(x ) converge a g'(x).
se x è un attrattore e |g'(x)| = q ¹ 0 allora | xn+k- x | @ qk | xn- x | per n grande; si parla di convergenza lineare di coefficiente q.
se x è un attrattore e |g'(x)| = 0 allora | xn+1- x | = | g(xn)- g(x) | = g"(x ) ( xn- x )2 / 2 converge a g"(x)/2.
Dunque | xn+k- x | / | xn- x |2 @ (g"(x)/2)k per n grande; si parla di convergenza quadratica.
Il metodo di Newton è a convergenza quadratica poiché g'(x) = f(x) f"(x)/ (f'(x))2 = 0 Û f(x)=0, a meno che la soluzione non sia n-pla e allora è a convergenza lineare di coefficiente (n-1)/n.
Per quanto riguarda la velocità di convergenza, quando x è un attrattore e le derivate prima e seconda g', g'' sono continue, si possono distinguere almeno due casi.
Poiché | xn+1- x | / | xn- x | = | g(xn)- g(x) | / | xn- x | = g'(x ) allora:
se |g'(x)| = q ¹ 0 allora | xn+k- x | @ qk | xn- x | per n grande; si parla di convergenza lineare di coefficiente q;
se invece g'(x) = 0 ma g''(x) ¹ 0 allora | xn+1- x | = | g(xn)- g(x) | = g"(x ) ( xn- x )2 / 2 e dunque | xn+k- x | / | xn- x |2 @ (g"(x)/2)k per n grande; si parla di convergenza quadratica.
Il metodo di Newton è a convergenza almeno quadratica poiché g'(x) = f(x) f"(x)/ (f'(x))2 = 0 dal momento che f(x)=0, a meno che la soluzione non sia n-pla e allora è a convergenza lineare di coefficiente (n-1)/n.
Occorre dire infine che nella pratica si usano comunque metodi misti. E' bene associare ai metodi opportune rappresentazioni grafiche; almeno per individuare intervalli [a,b] per cui f(a)·f(b)<0, per valutare la possibilità che f' sia sempre dello stesso segno sull'intervallo contenente lo zero (funzione monotona) o che f" sia sempre dello stesso segno sull'intervallo contenente lo zero (funzione con la stessa concavità).
Bibliografia
Engel A., Mathematiques et informatique, Cedic/Nathan, Paris 1985
Stoer J.,Introduzione all'analisi numerica, vol.1, Zanichelli, Bologna 1976
Vilenkin N.Ya., Method of successive approximations, Mir Publisher, Moscow 1979
Di seguito sono riportate varianti per le varie funzioni o per descrivere con la calcolatrice TI-92 i vari metodi.
La seguente funzione TI-92 rende possibile iterare una funzione un numero di volte pari a un numero naturale fine>1 o fino a raggiungere una approssimazione inferiore a un numero reale 0<fine<1
iterazio (espr,seme,fine)
Func
Local ii,lit
{seme}! lit
¦ se fine>1 lo considero n¬iterazioni
If fine>1 Then
For ii,2,fine
augment(lit,{espr|x=lit[ii-1]})! lit
EndFor
¦ altrimenti lo considero grado appros
ElseIf fine>0 and fine<1 Then
augment(lit,{espr|x=seme})! lit
2! ii
While abs(lit[ii]-lit[ii-1])>fine
augment(lit,{espr|x=lit[ii]})! lit
ii+1! ii
EndWhile
EndIf
Return lit
EndFunc
La funzione u1 è la successione dei punti ottenuti con il metodo di bisezione sull'intervallo [a,b]
{a,b,(a+b)/2}! u1
(u1(n-1)+sign(f(u1(n-3))*f(u1(n-1)))*u(n-2)+ sign(f(u1(n-2))*f(u1(n-1)))*u(n-3) )/(1+ sign(f(u1(n-3))*f(u1(n-1)))+ sign(f(u1(n-2))*f(u1(n-1))) ) ! u1(n)
Ad esempio si provi, definito f(x) = cos(x)-x,
-1/2! a
1! b
seq(u1(n),n,1,10)
La funzione zeriBis ricorsiva è un'altra implementazione del metodo di bisezione
when(f(a)*f(b)<0, when(abs(f((a+b)/2))< e ,(a+b)/2, when(f(a)*f((a+b)/2)<0,zeriBis(a,(a+b)/2,e ),zeriBis((a+b)/2,b,e )))) § zeribis(a,b,e )
Ad esempio si provi, definito f(x) = cos(x)-x,
zeribis(0,2,10^-3)
In modo analogo per il metodo di falsa posizione:
when(f(a)*f(b)<0,when( abs( f((a*f(a)-b*f(b))/(f(a)+f(b))) ) )< e ,(a+b)/2,when(f(a)* f((a*f(a)-b*f(b))/(f(a)+f(b)))<0,falsaPos(a, (a*f(a)-b*f(b))/(f(a)+f(b)),e ),falsaPos((a*f(a)-b*f(b))/(f(a)+f(b),b,e )))) § falsaPos(a,b,e )
falsaPos(0,2,10^-3)
La seguente funzione TI-92 implementa ancora il metodo di bisezione ma fornisce una traccia dei passaggi in forma di matrice 3 x n°iteraz necessarie per raggiungere l'approssimazione richiesta.
zbisIter (ff,aa,bb,appr)
Func
Local esit,val,ii
approx(ff|x=(aa+bb)/2)! val
[["a",aa]["b",bb]["f((a+b)/2",val]]! esit
While abs(val)>appr
If approx(ff|x=aa)*val<0 Then
(aa+bb)/2! bb
Else
(aa+bb)/2! aa
EndIf
approx(ff|x=(aa+bb)/2)! val
augment(esit,[[aa][bb][val]])! esit
EndWhile
Return esit
EndFunc