Logica matematica
INTRODUZIONE
La logica, come scienza, nacque nella Grecia classica e, fin
dal suo sorgere, si trovo' in stretti rapporti con la matematica. La matematica
infatti, tende a costruire teorie deduttive molto rigorose e la logica vuole
essere appunto la scienza che fornisce all'uomo (e in particolare al matematico)
gli strumenti indispensabili per controllare la rigorosità' dei suoi
ragionamenti. Prenderemo spunto dal voler sapere cosa vuol dire ragionare ma
svilupperemo contemporaneamente la logica delle proposizioni e la logica dei
predicati.Applicheremo le nozioni apprese all'informatica e accenneremo alla
logica dei circuiti.
Saggio di logica matematica a cura del Prof. Alessandro Amodei
Per approfondimenti, domande o altro scrivere a:
LE FIGURE DI RAGIONAMENTO
Che vuol dire ragionare? Prendiamo spunto da situazioni abbastanza
frequenti nei normali rapporti quotidiani. Sentiamo cosa dice Giovanni ad un
amico.
a)Se mi fossi alzato presto ,avrei preso il treno in orario, ma purtroppo l'ho perso.
L'amico allora pensa tra se e se che Giovanni deve essersi alzato tardi.
b)Se Gianna amasse Federico, gli avrebbe telefonato ,ma
non lo ha
fatto. Cosa si può' dedurre?
c)Se finisce la benzina in un auto, la macchina si ferma. La macchina
non si e' fermata. Cosa si può' dedurre?
d)Gianni sapeva che se avesse studiato sarebbe stato promosso ma
purtroppo ciò' non e' stato. Cosa si può' dedurre?
In ogni esempio proposto ho chiesto cosa si può' dedurre. Ciò'
che si e' dedotto e' la conclusione ricavata da ciò' che veniva premesso.
Qualunque cosa si sia dedotto diremo di aver compiuto un ragionamento.
Diremo allora di compiere un ragionamento quando siamo in grado di ricavare
delle affermazioni come conseguenza di certe premesse.
Vediamo ancora un esempio di ragionamento:
d)Un camionista si ferma sul ciglio della strada con il camion che non intende ripartire. Il camionista pensa tra se e se che se finisce la benzina il camion si ferma e, dato che si e' fermato, dovrebbe essere finita la benzina.
Si dovrebbe osservare che qualcosa non va nella conclusione finale. Infatti il camion potrebbe essersi fermato per un guasto al motore o altro. Ancora un esempio:
Un candidato politico grida alla folla: "Se mi voterete ridurrò
le tasse".
Se le persone che ascoltano, intimorite e contente, pensano di votarlo per avere
meno tasse, si sarebbe d’accordo con tale conclusione? Si potrebbe obbiettare
dicendo che, anche se si votasse qualche altro candidato, si potrebbero avere
meno tasse da pagare. Non tutti i ragionamenti conducono a conclusioni corrette.
Come facciamo a essere sicuri che ciò' che ricaviamo dalle nostre premesse
e' corretto?
Nella vita di tutti i giorni l'essere umano e' chiamato a prendere decisioni
e modificare il proprio comportamento sulla base di informazioni derivantegli
da deduzioni di tale genere.
E’ quindi fondamentale essere in grado di stabilire se le nostre deduzioni
sono corrette ossia affidabili in vista delle conseguenze che possono derivare
dal crederle tali.
Osserviamo cosa hanno in comune i ragionamenti a) b) c).
Se tralasciamo ciò' di cui si parla e ci soffermiamo solo sullo scheletro delle proposizioni che compongono le premesse, notiamo che per i tre esempi si ha :
1) Se p allora q
non q
--------
non p
Sono state sostituite delle lettere al posto delle proposizioni
come "alzarsi
presto e prendere il treno in orario, la benzina finisce ecc" e ciò'
che risulta e' lo
scheletro, non solo delle proposizioni, ma anche del ragionamento.
"Se p allora q" e' detta forma condizionale, mentre
p e q sono dette variabili proposizionali.
La forma "non p" e' la negazione di p.
Le proposizioni degli esempi hanno diverso significato per noi ma hanno tutte la stessa forma. Nel complesso si ha che una figura di ragionamento e' generalmente composta da più' forme proposizionali. Qual e' la figura di ragionamento dell'esempio d)?
2) Se p allora q
q
------------
p
Dagli esempi proposti abbiamo osservato che non tutte le figure
di
ragionamento sembrano portare a conclusioni corrette. Il lavoro che ci aspetta
consiste nel costruire delle tecniche per decidere se una figura di ragionamento
porta a conclusioni corrette. Ci occuperemo delle figure di ragionamento e
delle forme proposizionali in esse contenute e analizzeremo la figura indipendentemente
dal
significato che potremmo attribuire alle variabili proporzionali di cui ogni
forma e' composta.
La figura 1) ci ha condotto a conclusioni corrette. Sembra che
qualunque cosa metta al posto di p e q ,la conclusione sia corretta. Vediamo
il seguente esempio:
Poniamo: p="2 e' pari"; q="2 e' divisibile per 3".
Si ha :
Se 2 e' pari allora 2 e' divisibile per 3
ma 2 non e' divisibile per 3,quindi
-------------------------------------
2 non e' pari.
La conclusione e' in evidente contraddizione con la proposizione p="2 e'
pari". Eppure la figura sembrava condurre a conclusioni corrette. Il difetto
non sta nella figura in se ma nel fatto che una delle premesse ,cioè'
q="2 e' divisibile per 3" e' falsa. Dobbiamo allora fare attenzione
alla figura di ragionamento ma anche al
fatto che le premesse in essa contenute siano proposizioni vere.
Diamo allora la seguente definizione:
Una figura di ragionamento e' valida se, partendo da premesse
vere, conduce a conclusioni vere.
La conclusione dedotta da una figura di ragionamento valida si dice corretta.
PROPOSIZIONI SEMPLICI E COMPOSTE.
Occupiamoci ora delle proposizioni che compongono i nostri ragionamenti e osserviamo
come sono costruite. Con esse si afferma l'esistenza di un rapporto tra soggetti,
si afferma la presenza di una proprietà' di un soggetto o di un oggetto
ecc..
Nell'insieme delle espressioni linguistiche che possiamo costruire, come facciamo
a distinguere le proposizioni da quelle che non lo sono?
Esaminiamo le seguenti espressioni linguistiche:
1)Dante e' stato un grande poeta;
2)La terra e' piatta;
3)L'intero 6 e' divisibile per 2 e per 3;
4)5 e' pari;
5)2+3=7
6)un numero intero e' primo oppure ha divisori propri.
7)Se il discriminante dell'equazione ax2+bx+c=0 e' maggiore di zero, l'equazione
ammette soluzioni reali.
8)L'automobile catechizzo' l’ascensore.
Alcune espressioni tra quelle proposte sono vere , altre false e quindi le diremo proposizioni. L'espressione 8) non ha senso per noi e' quindi non e' una proposizione.
DEFINIZIONE:
Diremo "proposizione" una espressione linguistica
vera o falsa.
Non ci sembra strano dire che una affermazione e' vera o falsa, tanto siamo
abituati a farlo. Cosa vuol dire che una affermazione e' vera o falsa? Si e'
in grado di
stabilire se sono vere o valse le seguenti proposizioni?
a)"Dio esiste";
b)"La terra gira intorno al sole";
c)"Il fuoco brucia".
Molte delle nostre verità' o falsità' sono constatate direttamente,
ad altre ci
crediamo per fiducia in chi le afferma, altre ancora le accettiamo per fede.
Se non
vogliamo addentrarci in disquisizioni filosofiche su ciò che l'argomento
comporta
partiamo dall'accettare come intuitivo il significato di verità o falsità
che attribuiamo alle nostre affermazioni.
PROPOSIZIONI COMPOSTE
Consideriamo la proposizione "Il cavallo e' un quadrupede".
Non possiamo scomporla in "Il cavallo e'" e "un quadrupede"
perché tali espressioni non hanno senso e pertanto "Il cavallo e'
un quadrupede" e' detta proposizione semplice.
Possiamo costruire anche proposizioni composte come:
1)6 e' pari e 6 e' divisibile per 3;
2)un triangolo isoscele ha due lati uguali e due angoli uguali;
3)un numero intero e' pari oppure dispari;
4)se un numero e' pari allora e' divisibile per due ecc.
Se prendiamo ad esempio la prima proposizione, si può scomporla in "6
e'
pari" e "6 e' divisibile per 3" che risultano entrambe proposizioni
e questa volta
semplici. Una tale proposizione e' detta composta.
LE FORME PROPOSIZIONALI
Abbiamo diversi esempi di proposizioni composte e questo ci suggerisce di analizzarne
lo scheletro per individuare la diversa composizione. Se sostituiamo le proposizioni
semplici con delle lettere ,che chiameremo variabili proposizionali, rimane
lo scheletro della proposizione che chiameremo forma proposizionale.
Analizziamo piu' attentamente le forme di alcune proposizioni.
1)Se Giovanni si alza presto allora prende il treno
in orario;
2)Lanciando un dado regolare ,l'esito e' pari oppure dispari;
3)Studio e guardo la televisione;
4)Un numero e' pari se e solo se e' divisibile per due;
5)Non mangio;
Se sostituiamo alle proposizioni semplici "Giovanni si alza presto, Giovanni prende il treno in orario, l'esito e' pari, ecc.." con delle lettere si arriva alle forme proposizionali seguenti:
1)Se p allora q;
2)p o q;
3)p e q;
4)p se e solo se q;
5)non p.
A tali forme daremo dei nomi appropriati.
a)La forma "se p allora q " si dira' forma condizionale;
b)La forma "p o q" si dira' forma alternativa o anche alternativa
logica;
c)La forma "p e q " si dira' forma congiuntiva o congiunzione logica;
d)La forma "p se e solo se q" si dira' forma bicondizionale;
e)La forma " non p" si dira' negazione di p o forma negativa.
NOTAZIONI: Decidiamo di indicare con :
a)p->q la forma "se p allora q";
b)p+q la forma "p o q";
c)pq la forma "p e q";
d)p<->q la forma "p se e solo se q";
e) -p la forma "non p"
Chiameremo connettivi logici cio' che lega le variabili proposizionali. I
connettivi logici presentati sono:
a)Il condizionale :"-> ";
b)L'alternativa "+" che diremo "somma logica";
c)La congiunzione " " che diremo "prodotto logico";
d)Il bicondizionale "<->";
e)La negazione di p "-p" che diremo "negazione logica";
UN PARALLELO TRA INSIEMISTICA E LOGICA.
Non e' difficile pensare all'insieme delle proposizioni semplici come ad un
insieme qualunque di enti che possono assumere due valori "vero o falso".
Possiamo pensare ai connettivi logici come a delle operazioni nell'insieme delle
proposizioni semplici che compongono due proposizioni per ottenere una proposizione
composta.
Tentiamo allora un parallelo tra insiemistica e logica che ci sara' di aiuto
per il seguito. In insiemistica abbiamo definito le operazioni di unione, intersezione,
differenza, complementare, differenza simmetrica e prodotto cartesiano. Alla
luce di quanto detto, possiamo osservare che tali operazioni erano assegnate
mediante
forme proposizionali. Se la forma risultava vera per una valore della variabile
proposizionale, l'elemento apparteneva all'insieme , altrimenti, se risultava
falsa, non vi apparteneva. Ecco un importante modo di agganciarsi a quanto gia'
fatto, un naturale prolungamento di quanto gia' detto. In insiemistica si parlava
di insieme vuoto e abbiamo detto allora che bastava una proposizione sempre
falsa per
assegnarlo. In logica troviamo le proposizioni sempre false che diremo contraddizioni.
In insiemistica abbiamo parlato dell'insieme ambiente o universo che veniva
assegnato da una proposizione sempre vera .In logica diremo una tale proposizione
una tautologia. In insiemistica un elemento poteva appartenere o no all'insieme
,in logica cio' corrisponde al fatto che una proposizione puo' essere vera o
falsa. Se continuiamo con questo parallelo tra insiemistica e logica e' facile
sviluppare l'argomento successivo che riguarda l'analisi della verita' delle
forme proposizionali.
LE TAVOLE DI VERITA' DELLE FORME PROPOSIZIONALI.
In questo paragrafo vogliamo stabilire quando una forma proposizionale e' vera
o falsa a partire dai valori di verita' delle variabili proposizionali. Analogamente
a quanto visto in insiemistica a proposito delle tavole di appartenenza, riproponiamo
in questa sede, per le forme proposizionali, le tavole di verita'.
LA TAVOLA DI VERITA' DELLA FORMA "P+Q" O SOMMA
LOGICA.
Iniziamo proprio dalla forma p+q .A quale operazione insiemistica si riferisce?
Dovrebbe essere semplice la risposta "all'unione tra insiemi". Ricordiamo
come è definita l'unione tra due insiemi A e B.
Un elemento appartiene all'unione se appartiene ad A oppure a B.
Se pensiamo ora di associare l'appartenenza ad A alla verita' di una variabile
proposizionale e cosi' anche per B otteniamo la tavola di verita' della somma
logica in modo del tutto naturale. Indicheremo sempre con "1" la verita'
di una variabile proposizionale (come indicavamo con "1" l'appartenenza
all'insieme) e con "0" la
falsita' (in modo analogo si indicava con "0" la non appartenenza
ad un insieme). Si ha allora la tavola della somma logica come abbiamo fatto
per la tavola dell'appartenenza:
|
p
|
q
|
p+q
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
La tavola mette in evidenza che la forma proposizionale "p+q" e'
vera se almeno una delle variabili e' vera, ed e' falsa se entrambe sono false.
Analogamente, in insiemistica, un elemento apparteneva all'unione tra due insiemi
A e B se l'elemento apparteneva ad almeno uno dei due insiemi. Non apparteneva
all'unione se l'elemento non apparteneva ne' ad A ne' a B. Parliamo di enti
diversi come insiemi e proposizioni, di operazioni diverse come unione e somma
logica ma non dovrebbe sfuggire a nessuno lo stretto rapporto tra essi.
UGUAGLIANZA INSIEMISTICA E EQUIVALENZA LOGICA
Un ulteriore parallelo si puo' porre ricordando che due insiemi A e B ottenuti
mediante operazioni insiemistiche da altri insiemi, possono risultare uguali,
in
funzione dell'appartenenza o no di un elemento agli insiemi componenti. Cio'
accade
se un elemento che appartiene ad A appartiene anche a B e se un elemento che
non
appartiene ad A non appartiene a B. In logica, se due forme proposizionali sono
entrambe vere o entrambe false in corrispondenza dei valori di verita' delle
variabili
proposizionali, si dicono equivalenti. L'equivalenza tra p e q si indichera'
al solito
modo con p=q.
Proprietà della somma logica.
Vediamo ora quali proprieta' valgono per la somma logica. L'operazione di
somma logica gode delle stesse proprieta' dell'unione e cioe':
1)idempotenza :p+p=p;
2)commutativa: p+q=q+p;
3)associativa: p+(q+r)=(p+q)+r=p+q+r;
Inoltre se indichiamo con "0" le contraddizioni (proposizioni sempre
false) e con "1" le tautologie (proposizioni sempre vere) si ha :
4)p+0=p; (in insiemistica AUø=A):
5)p+1=1; (in insiemistica AUR=R essendo R l'insieme ambiente).
Non e' difficile dimostrare queste proprieta' in modo analogo a quanto gia'
visto in insiemistica. Il modo per decidere se due forme proposizionali sono
equivalenti e' quello di confrontare le sequenze di "0" e "1"
nelle rispettive colonne.
Se tali sequenze sono uguali le forme sono equivalenti.
LA TAVOLA DI VERITA' DELLA FORMA "PQ" O PRODOTTO
LOGICO
Possiamo passare ora all'operazione di prodotto logico che corrisponde
all'operazione di intersezione tra insiemi. Ecco la tavola di verita' della
congiunzione, identica a quella di appartenenza dell'intersezione:
|
p
|
q
|
pq
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
La tavola mette in evidenza che la forma"pq" e' vera se entrambe
le variabili
sono vere ed e' falsa se almeno una delle variabili e' falsa.
Analogamente in insiemistica un elemento apparteneva all'intersezione tra
due insiemi A e B se apparteneva sia ad A che a B. Non apparteneva all'intersezione
se apparteneva ad A ma non a B oppure a B ma non ad A oppure ancora se non apparteneva
ne' ad A ne' a B.
Per il prodotto logico, valgono le stesse proprieta' dell'intersezione e cioe:
1)idempotenza:pp=p;
2)commutativa: pq=qp;
3)associativa: p(qr)=(pq)r=pqr;
Inoltre si ha:
4)p0=0 (in insiemistica Aø=ø);
5)p1=p (in insiemistica AR=A ,essendo R l'insieme ambiente)
Valgono anche le proprieta' distributive della somma rispetto al prodotto e
viceversa:
6)a(p+q)=ap+aq;
7)a+(pq)=(a+p)(a+q).
Valgono le leggi di assorbimento:
8)a(a+q)=a;
9)a+(aq)=a;
LA TAVOLA DI VERITA' DELLA NEGAZIONE LOGICA:
La negazione logica e' associata all'operazione di complementare di un
insieme ed ha la stessa tavola di verita'. Bisogna aggiungere qualcosa di importante
da cui scaturisce la tavola che costruiremo.
La logica comune, cioe' la nostra logica, e' basata su due principi
fondamentali:
1) Principio del terzo escluso:
Una proposizione o e' vera o e' falsa e non altrimenti;
2)Principio di non contraddittorieta':
Una proposizione vera non puo' essere contemporaneamente anche falsa.
Su questi principi basiamo la nostra logica a due valori . Ecco allora la tavola
della negazione logica:
|
p
|
-p
|
|
0
|
1
|
|
1
|
0
|
Come notiamo e' simile alla tavola di appartenenza dell'insieme complementare di un insieme A (che ricordiamo e' sempre considerato s.i. di un insieme ambiente R). Se un elemento apparteneva ad A non apparteneva al complementare di A e viceversa.
Valgono le importanti leggi di De Morgan (come in insiemistica):
1) -(-p)=p cioè la doppia negazione afferma!!;
2) -(p+q) = (-p)(-q) cioè la negazione di p oppure q equivale alla congiunzione delle negazioni;
3) -(pq) = (-p)+(-q) cioè la negazione della congiunzione è l'alternativa tra le negazioni.
Esempi:
Affermare che "non è vero che non piove" equivale ad affermare che piove!!
Attenzione quindi ad usare espressioni del tipo "non ho studiato niente" perchè il senso logico è che avete studiato tutto!!!!
Negare che "oggi piove o c'è il sole" equivale a dire che "non piove e non c'è il sole";
Negare che "il lavoro nobilita l'uomo e lo rende simile ad una bestia" equivale a dire che "il lavoro non nobilita l'uomo o non lo rende simile ad una bestia".
Inoltre si ha:
4) -p+(p)=1 cioe' una tautologia (cioè sempre vera);
5) -p(p)=0 cioe' una contraddizione (cioè sempre falsa).
LA TAVOLA DI VERITA' PER LA FORMA CONDIZIONALE P->Q.
La forma condizionale "se..allora..." e' forse la forma
piu' usata nel linguaggio
comune. E' necessario osservare pero' in quale contesto e' usata.
Diciamo ad esempio:
1)Se piove e sono senza ombrello allora mi bagno;
2)Se un numero e' pari allora e' divisibile per due;
3)Se un triangolo ha due soli lati uguali allora e' isoscele.
Non ci sogneremmo di dire invece:
4)Se il cavallo e' un quadrupede allora la farfalla vola;
5)Se Dante ha scritto la divina commedia allora la terra gira intorno al
sole.
Le proposizioni 4) e 5) potranno farci sorridere pero' anche esse hanno
senso di esistere,mentre per tutti hanno senso le rimanenti proposizioni.
Per questo distingueremo tra condizionale logico e condizionale
materiale.
Gli esempi 1) 2) 3) li diremo condizionali logici in quanto, il verificarsi
della
prima proposizione che e' detta premessa, porta al verificarsi della seconda
proposizione, che e' detta conseguenza. Diremo condizionali materiali le proposizioni
degli esempi 4) e 5). Noi usiamo comunemente il condizionale quando vogliamo
stabilire un
rapporto di causa e effetto tra due proposizioni. Dovendo esaminare la forma
proposizionale indipendentemente dai valori di verita' delle variabili proposizionali,
dovremo fare riferimento al condizionale materiale ,che e' la forma piu' generale
con cui si puo' porre il condizionale. Decidiamo di chiamare antecedente la
proposizione "p" e conseguente la proposizione "q". Per
costruire la tavola di verita' della forma condizionale partiamo da un semplice
esempio.
Supponiamo che vi chieda di prendermi un libro in biblioteca e vi dica:
vorrei un libro dalla biblioteca pero', se e' di matematica allora deve trattare
di
logica. E' chiaro che porteremo un libro quando riterremo vera la proposizione
che
ho assegnata .Vediamo allora caso per caso come ci dobbiamo comportare.
Poniamo: p= libro di matematica e q= libro di logica.
Otteniamo quanto segue:
|
p
|
q
|
p->q
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Perche' abbiamo posto "1" nel primo caso?
Ho posto la condizione che se il libro era di matematica doveva trattare di
logica quindi, se non e' di matematica, puo' essere qualunque cosa.
Ecco perche' ho posto "1" nella prima riga e nella seconda. Spero
che risulti
chiaro al lettore, che deve riflettere un po' su quanto detto.
Passiamo al terzo caso.
Se il libro e' di matematica ma non tratta di logica allora non lo
prendiamo perche' contraddice cio' che vi ho chiesto.
Questo dovrebbe essere piu' facile. Infine e' banale anche il quarto caso e
cioe' se il libro e' di matematica e di logica verra' preso.
Da questo dobbiamo ricordare che il condizionale materiale e' falso solo nel
caso in cui l' antecedente e' vero e il conseguente e' falso. In ogni altro
caso il
condizionale e' vero.
FORMA EQUIVALENTE DEL CODIZIONALE
La forma condizionale ha una sua forma equivalente molto importante che
cercheremo di ricavare. Partiamo dal voler negare la forma p->q. Dalla tavola
troviamo che il condizionale e' falso solo nel caso in cui l'antecedente e'
vero e il
conseguente e' falso. Se e' falso il condizionale e' vera la negazione che avra'
la forma: -p (q).
La negazione di "Se corro allora sudo" e' "Corro e non sudo".
La negazione di "Se un numero e' pari allora e' divisibile per due"
e' "Un
numero e' pari e non e' divisibile per due".
Se chiediamo a qualcuno di negarci la proposizione: se mangio allora mi
sazio, dovra' risponderci dicendo: mangio e non mi sazio.
Poniamo allora la seguente equivalenza logica: -(p->q)= p(-q)
Dato che la doppia negazione afferma, come dice la prima legge di De
Morgan, dalla precedente otteniamo una forma equivalente al condizionale:
p->q= -p + q
Quindi dire "se corro allora sudo" e' equivalente
a dire "non corro oppure
sudo". L'equivalente di "se mangio allora mi sazio " e' "non
mangio oppure mi
sazio".
ALTRE FORME CONDIZIONALI: IL CONTRARIO
Spesso facciamo confusione tra fare il contrario di una proposizione e fare
la
negazione. Se chiedo a qualcuno di negare la proposizione "se corro allora
sudo",
spesso mi sento rispondere con " se non corro allora non sudo", mentre
dovrebbe
dire "corro e non sudo". Che tipo di risposta mi ha offerto l'interlocutore?
Questo tipo di affermazione e' detto il contrario.
ATTENZIONE !!
Confondere il contrario con la negazione e' un gravissimo errore logico.
Il contrario di "uomo" è "donna", oppure "non
donna".
Il contrario di "essere pari "e' "essere dispari", oppure
"non pari".
Le frasi hanno lo stesso significato. Esaminiamo i seguenti casi:
Il contrario di "bello" e' "brutto" pero' la negazione di
"bello" e' "non bello" che
non ha lo stesso significato. Nei primi due esempi abbiamo lo stesso risultato
logico, nel terzo no. Questo perche' nei primi due casi potevamo avere solo
due alternative, mentre per la bellezza abbiamo una gradazione che va dal "bello
al brutto" attraverso il "bellino", "belloccio" e via
dicendo. In questo caso comprendiamo lo scopo del contrario e della negazione.
Il contrario associa i due elementi opposti dell'attributo che nominiamo mentre,
la negazione, essendo equivalente al complementare insiemistico, vi individua
la classe complementare.
Non dobbiamo quindi confondere il contrario con la negazione, essendo due
aspetti logici completamente diversi
Altri esempi:.
Il contrario di: p+q e' (-p)+(-q),
La negazione di: p+q e' (-p)(-q).
Il contrario di: pq e' (-p)(-q) ,
La negazione di: pq e' (-p)+(-q)
Il contrario di: p->q e' (-p)->(-q);
La negazione di: p->q e' p (-q).
Se diciamo ad esempio :
"se un numero e' divisibile per sei e' anche divisibile per due",
Il contrario e' " se un numero non e' divisibile per 6 allora non e' divisibile
per
due.
La negazione invece e' "un numero e' divisibile per 6 e non per 2".
La prima affermazione e' vera e risulta cosi' falsa la negazione. Cosa
possiamo dire del contrario? Se prendiamo ad esempio, "4", esso non
e' divisibile per "6" pero' e' divisibile per "2" e quindi
il contrario e' falso. Quindi anche il contrario e' falso come la negazione,
ed e' questo forse il motivo per cui spesso vengono confusi.
Oltre al contrario, per un condizionale si possono costruire altre forme:
IL CONDIZIONALE INVERSO:
Dato il condizionale p->q si dice condizionale inverso il condizionale: q->p.
L'inverso si ottiene scambiando l'antecedente con il conseguente. Se il condizionale
p->q e' vero, non e' detto che lo sia anche il condizionale inverso: L'affermazione:
"se
abito a Firenze allora abito in Toscana" e' vera. L'inverso :"se abito
in Toscana allora
abito a Firenze" e' falso. Vi sono comunque dei casi in cui, se e' vero
p->q, e' vero
anche q->p. L'affermazione: se un numero e' pari allora e' divisibile per
due" e' vera.
L'inverso: "se un numero e' divisibile per due allora e' pari" e'
ancora vero.
Vediamo ancora una terza forma condizionale ottenibile dal condizionale p->q:
IL CONDIZIONALE CONTRONOMINALE
Dato il condizionale p->q, possiamo formare il condizionale: (-q)->(-p)
ottenuto invertendo il verso dell'implicazione e negando le proposizioni p e
q.
Possiamo osservare che se p->q e' vero lo e' anche il contronominale. Le
affermazioni: "se abito a Firenze allora abito in Toscana" e "se
non abito in Toscana
allora non abito a Firenze" sono entrambe vere.
Il contronominale e' quindi una importante equivalenza logica di un condizionale.
LA TAVOLA DI VERITA' DEL BICONDIZIONALE
Abbiamo visto che il condizionale p->q e il condizionale inverso q->p
non
sono entrambi veri o entrambi falsi (in generale). Vi sono pero' dei casi (come
abbiamo visto) in cui cio' accade. E' possibile pertanto costruire una nuova
forma
proposizionale, il bicondizionale, che risulta vera o falsa a seconda che siano
entrambi veri o falsi i due condizionali. Scriveremo p<->q e leggeremo
p se e solo se
q per esprimere il fatto che p->q e q->p sono entrambi veri o entrambi
falsi. Il
bicondizionale e' allora equivalente a (p->q) (q->p) cioe': p<->q=(p->q)(q->p)
Il bicondizionale è vero quindi se sono o entrambe vere o entrambe false
le proposizioni componenti. La tavola di verita' del bicondizionale e' allora:
|
p
|
q
|
p<->q
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
E' importante osservare che, nel linguaggio comune e soprattutto nel
linguaggio matematico, troviamo il condizionale diretto e inverso e il bicondizionale
formulato a parole in modo diverso. Ci capita spesso di sentir dire: "condizione
necessaria ma non sufficiente per vivere e' respirare" oppure "e'
necessario
respirare per vivere". Con cio' intendiamo affermare che "se non respiriamo
allora
non possiamo vivere" o, equivalentemente "se viviamo allora respiriamo".
Dire
allora che p e' necessario per q vuol dire affermare la verita' del condizionale
q->p. E' facile capire che respirare non e' sufficiente per vivere in quanto
occorre
anche mangiare, bere e via dicendo.
Se respirare non e' sufficiente per vivere e' falso il condizionale inverso
p->q.
Consideriamo l'esempio seguente: "e' sufficiente avere un diploma per
trovare un lavoro". Cio' equivale ad affermare che "se ho un diploma
posso
trovare un lavoro".
Dire allora che p e' sufficiente per q vuol dire affermare la verita' del
condizionale p->q.
La condizione pero' non e' necessaria in quanto, se trovo un lavoro, non e'
necessariamente detto che abbia un diploma. Anche in tal caso il condizionale
inverso e' falso.
Esaminiamo infine la seguente affermazione:
condizione necessaria e sufficiente perche' un triangolo sia isoscele e'
che abbia due angoli uguali.
Con cio' dobbiamo intendere che:
Se un triangolo ha due angoli uguali e' isoscele (condizione
necessaria); se un triangolo e' isoscele ha due angoli uguali (condizione
sufficiente).
Scopriamo cosi' che tale modo di esprimersi equivale ad all'affermazione:
un triangolo e' isoscele se e solo se ha due angoli uguali e quindi ci
esprimiamo mediante una forma bicondizionale.
Dire allora che p e' condizione necessaria e sufficiente per q equivale ad
affermare la verita' o la fasita' contemporanea dei due condizionali:
p->q e q->p ossia p<->q.
ANALISI DELLE FIGURE DI RAGIONAMENTO
Riprendiamo una delle figure presentate e cioe':
p->q
-q
------------
-p
Dobbiamo ritenere vere le premesse e pensare quindi che sia vera
la loro
congiunzione.Dalle premesse deve conseguire la verita' della conclusione. Possiamo
scrivere allora la figura di ragionamento come una unica forma proposizionale
come
segue:
(p->q)(-q)->(-p)
|
p
|
q
|
-p
|
-q
|
p->q
|
(p->q)(-q)
|
(p->q)(-q)->(-p)
|
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
Osserviamo che la forma finale della tavola risulta essere sempre vera cioe'
una tautologia. Da questo dobbiamo ricordare che:
Una figura di ragionamento e' valida se ,la forma proposizionale ottenuta congiungendo
le premesse e implicando la conclusione risulta essere una tautologia.
Siamo ora in grado di analizzare una figura di ragionamento per stabilire se
e' o no una tautologia.
Riprendiamo ad esempio la seconda forma presentata nel primo paragrafo del
capitolo e cioe':
p->q
q
-------
p
Verifichiamo con la tavola di verita' che tale figura di ragionamento
non e'
valida. La figura di ragionamento equivale alla forma proposizionale:
(p->q) (q)->p
e quindi:
|
p
|
q
|
p->q
|
(p->q)(q)
|
(p->q)(q)->(p)
|
|
0
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
1
|
1
|
1
|
Osservando la colonna relativa alla forma finale della tavola vediamo
bene che non si ha una tautologia. Questa forma e' spesso usata nelle scienze
empiriche come la fisica e rappresenta la base su cui si fonda il metoto ipotetico
deduttivo che e' usato per
acquisire conoscenze. Nel corso di fisica avete spesso usato questa forma per
stabilire ad esempio se una certa ipotesi e' corretta o no. Supponiamo di ipotizzare
che un certo fenomeno sia dovuto a certe cause e teoricamente prevediamo che,
se
l'ipotesi fatta e' corretta, si dovrebbero osservare certe conseguenze. In laboratorio
simuliamo il fenomeno e riscontriamo la presenza delle conseguenze previste.
Possiamo dedurre da cio' che l'ipotesi fatta e' corretta? L'insegnante di fisica
dovrebbe aver detto che tale ipotesi e' corretta "fino a prova contraria".
Questo
significa che le conseguenze potrebbero essere dovute all'ipotesi fatta ma anche
da
altre ipotesi (riga 2 della tavola).
Questo ci insegna un detto importante tipico delle scienze empiriche e cioe':
Non sono sufficienti infinite prove per confermare una teoria ma e'
sufficiente una controprova per rifiutarla.
Questo metodo e' usato da tutti noi per formulare congetture circa l'esistenza
di rapporti tra fatti osservati. Le nostre conoscenze si basano sulla verifica
parziale
delle conseguenze previste da una congettura e non possiamo mai essere certi
che
tali congetture siano vere in assoluto. Se prevediamo che il toccare il fuoco
provoca
dolore cio' e' dovuto al fatto che, da esperienze passate, abbiamo riscontrato
questa
conseguenza. Cio' dipende dalle leggi fisiche del luogo in cui viviamo. Se tali
leggi
fisiche dovessero cambiare cambierebbero anche le conseguenze e quindi, di
conseguenza anche le nostre conoscenze, ma il metodo di apprendere rimarrebbe
lo
stesso. Provate a verificare la validità della seguente forma di ragionamento:
p->q
q->r
---------
p->r
Questa figura di ragionamento e' spesso usata in matematica,
ad esempio quando si
risolve un'equazione. Infatti se vogliamo stabilire quando e' vera la proposizione,
x+4=8, si ha: x+4=8->x=8-4; x=8-4->x=4. Quindi x+4=8->x=4.
APPLICAZIONI DELLA LOGICA ALL'INFORMATICA
E' di fondamentale importanza conoscere in che modo le nozioni apprese
possono essere applicate in informatica. I connettivi logici studiati sono implementati
in quasi tutti i linguaggi di programmazione , anche se sono presenti con notazioni
diverse.Il connettivo "oppure" che abbiamo indicato con "+"
,e' indicato con "OR". Il
connettivo "e" che abbiamo indicato con " " ,e' indicato
con "AND". Il connettivo "non"
,che abbiamo indicato con "-" e' indicato con "NOT".
E' presente anche il consizionale "SE ...ALLORA" che noi abbiamo indicato
con "-->" ed e' indicato con "IF .. THEN..". Sono implementati
anche altri connettivi,
anche se non in tutti i linguaggi come il connettivo "NOR" o somma
negata e il
connettivo "NAND" o congiunzione negata.
In informatica uno dei problemi che più spesso si pone è la gestione
degli archivi (data-base):
Gestire un archivio di dati vuol dire non solo memorizzarli in modo organico
ma saper trarre dall'archivio tutte le informazioni che occorrono. Il computer
è programmato a seguire le regole della logica esposte. Per ottenere
certe informazioni da un archivio un programmatore comunica al computer frasi
come:
IF (NOT p OR NOT q ) then (not r AND s).
Con le tavole di verità non sarebbe difficile sapere quali informazione vengono estratte.
Un computer è in grado e in breve tempo di analizzare la
frase e stabilire quali informazioni la rendono vera.
L'espressione trovata prende il nome di filtro e' serve per selezionare, tra
tutti i records di un file, quelli che soddisfano la condizione espressa dalla
forma
trovata e in cui compaiono solo i connettivi "or, and e not".
2. Supponiamo di disporre di un file fornitori.I campi di ogni record
siano:nome,citta',volume di vendite,eta'. Vogliamo selezionare tutti i fornitori
tali che:
Il fornitore abita a Firenze oppure se ha un volume superiore a 2000 unita'
allora ha 30 anni. Indichiamo con:
p=il fornitore abita a firenze;
q=il fornitore ha un volume di vendite superiore a 2000 unita';
r=il fornitore ha 30 anni.
Possiamo scrivere la richiesta nella forma seguente: p+(-q->r) che tradotta
in linguaggio informatico diventa: p OR(IF q THEN r).
LA LOGICA DEI PREDICATI
Nei capitoli precedenti abbiamo esaminato la logica delle forme
proposizionali costruite a partire dalle variabili proposizionali alle quali
potevamo
sostituire una proposizione,considerata come entita' atomica,non ulteriormente
scomponibile. Vogliamo ora analizzare le proposizioni nella loro struttura di
soggetto-
predicato. Consideriamo la proposizione:"il leone e' carnivoro". Il
soggetto e' "leone",
mentre, "l'essere carnivoro" e' un attributo del soggetto che chiameremo
predicato
unario. Consideriamo la proposizione:"l'intero 6 e' divisibile per 2".
In questa
proposizione si hanno due soggetti, mentre, "l'essere divisibile per",
risulta un
predicato binario.
Possiamo pensare a proposizioni i cui predicati risultino di arieta' qualunque,
ad esempio:Roma sta tra Napoli e Firenze. Il predicato, "stare tra"
e' ternario. In
insiemistica, mediante i predicati unari si assegnano degli insiemi.Per assegnare,
ad
esempio, l'insieme degli animali carnivori si scrive:
A={x/ x e' carnivoro}
L'espressione "x e' carnivoro" e' una forma proposizionale che abbiamo
considerato fino ad ora semplice e che vogliamo vederla composta da " x"
detta
variabile soggettiva e da "essere carnivoro" che e ' un predicato
unario. Se alla
variabile soggettiva si attribuisce un significato, la forma proposizionale
puo' o no
divenire una proposizione a seconda che sia vera o falsa. Un elemento appartiene
all'insieme se la proposizione che ne consegue e' vera altrimenti non vi appartiene.
Un modo diverso per trasformare una forma proposizionale in proposizione consiste
nell'uso dei quantificatori universale e esistenziale. Consideriamo infatti
un insieme
ambiente A i cui elementi siano animali carnivori e la forma predicativa "x
e'
carnivoro". Se scriviamo: per ogni x appartenente ad A , x è carnivoro
quello che si ottiene e' una proposizione vera anche se compare la variabile
soggettiva "x". Il termine "per ogni" si dice quantificatore
universale. Quando affermiamo invece che "almeno un uomo è onesto"
utilizziamo il quantificatore esistenziale (almeno ).
FORME EQUIVALENTI
I quantificatori possono essere espressi ciascuno mediante l'altro.
1)Se affermiamo che una proprieta' vale per tutti gli x allora non e' vero che
via
sia almeno un x per cui non valga.
Esempi:
Affermare che tutti i numeri pari sono divisibili per due, equivale ad affermare
che non vi e' alcun numero pari che non sia divisibile per due;
Affermare che tutti gli uomini sono mortali, equivale ad affermare che non vi
e' alcun uomo che non sia mortale.
Affermare che tutti i gatti sono mammiferi, equivale ad affermare che non vi
e' alcun gatto che non lo sia.
2)Se affermiamo che esiste almeno un x per cui vale una certa proprieta' ,cio'
equivale a dire che non e' vero che per ogni x non vale la proprieta' p.
Cioe':
Affermare che qualche numero naturale e' pari, equivale ad affermare che
non e' vero che tutti i numeri naturali sono non pari.
LA NEGAZIONE DEI QUANTIFICATORI
Se e' falso che una proprieta' p valga per ogni x allora esiste almeno un
x per cui p(x) non vale.
Non e' vero, ad esempio, che tutti gli studenti sono volenterosi, quindi e'
vero
che qualche studente non e' volenteroso.
Se e' falso che esiste almeno un x per cui valga p(x) cio' vuol dire che
per ogni x non vale la proprieta'p.
Non e' vero, ad esempio, che esiste un numero pari non divisibile per due,
quindi tutti i numeri pari sono divisibili per due. Se affermiamo che qualche
uomo
politico e' disonesto e vogliamo negarlo dovremo affermare che tutti gli uomini
politici
sono onesti .
I SILLOGISMI
Isillogismi sono considerati storicamente le figure di ragionamento per eccellenza.
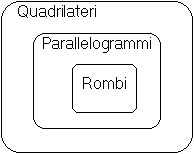
Un esempio di sillogismo:
Tutti i rombi sono parallelogrammi
Tutti i parallelogrammi sono quadrilateri
------------------------------------------
Tutti i rombi sono quadrilateri
Graficamente si ha:

Lo studio dei sillogismi (esistono ben quattordici forme diverse) è dovuto ad Aristotele. il quale Le forme di giudizio aristoteliche sono fondamentalmente quattro.
1)tutti gli x sono y;
2) nessun x e' y;
3)qualche x e' y;
4)qualche x non e' y.
Ogni sillogismo è composto da due premesse (come nell'esempio sopra riportato) espresso da una delle quattro forme da cuiscaturisce un giudizio esprimibile sempre in una delle solite quattro forme. Se consideriamo tre classi "a,b,c" , un sillogismo è composto da una premessa detta maggiore che stabilisce un rapporto tra a e b, la seconda premessa detta minore che stabilsce un rapporto tra b e c. Da queste scaturisce una conclusione che stabilisce un rapporto tra c e a. Esempio
ogni b è a (premessa maggiore)
ogni c è b (premessa minore)
-----------------------------
ogni c è a (conclusione)
Vi è però un forte legame tra la logica delle proposizione e
quella dei predicati.
Pensiamo all'insieme A delle figure geometriche e poniamo:
p=essere quadrilatero;
q=essere rombo;
r=essere parallelogramma.
Se x appartiene ad A, la forma sillogistica precedente puo' essere scritta
anche come
segue:
per ogni x app.A (p(x)->q(x))
per ogni x app. A (q(x)->r(x))
-------------------------
per ogni x app. A (p(x)->r(x))
Vediamo un altro esempio:
Sia p="essere pari" e q="essere divisibile per 2". L'affermazione
vera "tutti i
numeri pari sono divisibili per 2 " si puo' esprimere mediante la proposizione:
per ogni x [p(x)->q(x)]
Sia p="essere gatto" e q="essere uccello"
Il giudizio :nessun gatto e' un uccello, si puo' interpretare come una particolare
espressione del calcolo dei predicati. Si puo' affermare che "nessun gatto
e un
uccello scrivendo: non è vero che per ogni x (p(x)->q(x))
Si conclude che la logica aristotelica,
integrata dal calcolo proposizionale,
trova una completa sistemazione nell'ambito del calcolo dei predicati.
I CIRCUITI LOGICI.
Abbiamo fin'ora esaminato lo stretto legame tra insiemistica e logica delle
proposizioni. Abbiamo associato ad un insieme una proposizione; l'appartenenza
di
un elemento ad un insieme alla verita' di una proposizione. Alle operazioni
insiemistiche le operazioni logiche. Abbiamo riscontrato una identica struttura
cioe'
quella di ALGEBRA DI BOOLE. Vogliamo introdurre un nuovo tipo di enti che
possono essere avvicinati al concetto di insieme e di proposizione e cioe' I
CIRCUITI
LOGICI. Un circuito logico puo' essere pensato costituito da un generatore G
collegato ad un interruttore p(che puo' essere attivato o disattivato)e ad un
utilizzatore L (ad esempio ad una lampada che puo' essere spenta o accesa come
in
figura:
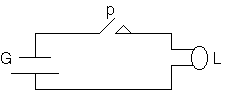
Lo stato della lampada e' subordinato allo stato dell'interruttore
nel circuito
elementare. Se l'interruttore e' sempre attivato,la lampada e' sempre accesa,se
l'interruttore e' sempre disattivato,la lampada e' sempre spenta. Se l'interruttore
puo'
essere attivato o disattivato ,la lampada puo' essere accesa o spenta. Troviamo
ancora una situazione in cui gli enti in oggetto possono assumere due stati,due
valori
(spento, acceso, attivato, disattivato) analogamente a quanto abbiamo visto
con
l'appartenenza di un elemento ad un insieme e alla verita' o falsita' di una
proposizione. Cominciamo a comprendere l'esistenza di svariate situazioni analoghe
che presentano cioe' le stesse caratteristiche. Ad esempio una porta puo' essere
aperta o chiusa, un rubinetto puo' versare acqua o non versarla e via dicendo.
CIRCUITI COMPOSTI
Se connettiamo due interruttori costruiamo un circuito composto che
determina lo stato della lampada connessa.Possiamo farlo come in figura:
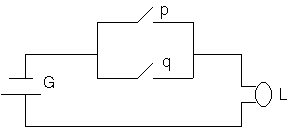
Lo stato della lampada L e' subordinato allo stato dei due interruttori
p e q.
Possiamo prevedere lo stato di L a partire dallo stato di p e q?
Se indichiamo con "0" lo stato spento per la lampada o disattivato
per
l'interruttore e con "1" lo stato opposto si ha:
|
p
|
q
|
L
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Si scopre facilmente osservando il circuito che la lampada e' accesa se almeno
uno degli
interruttori e' attivato e spenta se entrambi sono spenti e qualcosa ci ricorda
la tavola
di verita' della somma logica.
Diremo che gli interruttori sono collegati in PARALLELO.
Lo stato di L e' determinato dallo stato di p e q.
Possiamo sostituire il circuito precedente con uno simbolico che chiameremo
BLOCCO OR:
![]()
Possiamo studiare anche il circuito logico che equivale al prodotto logico come segue:
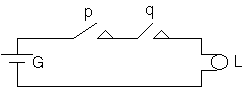
Lo stato di L e' determinato dallo stato di p e q nel seguente modo:
|
p
|
q
|
L
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Ancora troviamo che lo stato di L è condizionato dagli
stati di p e q secondo la tavola del prodotto logico. Solo se entrambi sono
attivati la lampada e'accesa. Diremo che gli interruttori
sono collegati in SERIE. Sostituiremo questo circuito
con il blocco logico :
che chiameremo BLOCCO AND.
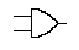
BLOCCO CORRISPONDENTE ALLA NEGAZIONE LOGICA:
I problemi logici non sono sempre il risultato di un'azione caratterizzata da
una relazione "positiva" rispetto ad un'altra.Ad esempio l'affermazione:
La lampada (L) si accende quando l'interruttore (p) non e' attivato implica
una opposizione tra l'accensione della lampada e l'attivazione dell'interruttore.
Si puo'
quindi affermare che quando l'interruttore e' attivato, esso impedisce l'azione
di
accensione della lampada. Possiamo scrivere:L=non p. L'operazione "negazione"
stabilisce semplicemente una relazione di opposizione,ossia stabilisce che,
quando p
e' vero, L e' falso; quando p e' 1, L e' 0. Un dispositivo che rappresenta tutto
questo
e' un rele' sotto raffigurato:
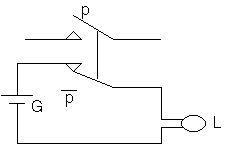
In figura i due interruttori p e non p sono collegati e si osserva
che quando p e' chiuso
allora non p e' aperto e quindi non p e' la negazione di p. Rappresenteremo
questo circuito
con un blocco detto blocco NOT, come in figura:
Quelli presentati sono i blocchi logici fondamentali. Possiamo
da questi
costruirne altri mediante una loro combinazione.
APPLICAZIONI
Vediamo ora quali applicazioni si possono avere con l'uso dei blocchi logici.
Esempi:
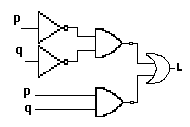
1.In una abitazione e' frequente accendere una lampada da due posti. Se p e
q sono gli interruttori supponiamo che si voglia la lampada accesa secondo lo
schema in tabella:
|
p
|
q
|
L
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Osservando la tavola della verita' si rileva che la lampada L e' accesa quando
i contatti p e q
sono disattivati oppure entrambi attivati. L'espressione per L e': L=pq+(-p)(-q)
Il circuito corrispondente e' allora:
Questi blocchi logici sono realizzati mediante circuiti elettronici e costituiscono i componenti fondamentali dei noti chip mediante i quali si realizzano le schede elettroniche base del funzionamento di quasi tutte le apparecchiature elettroniche e fondamentalmente dei computer.
Sulla logica e sulle conseguenze culturali che da essa scaturiscono si possono solo intravvedere alcune tracce in questo semplice trattato. Vorrei terminare con una osservazione importante. Le conquiste culturali dell'uomo sono fondamentalmente tre: il linguaggio, la logica, la conoscenza scientifica.
Attraverso il linguaggio possiamo comunicare e scambiarci informazioni. Ciò di cui parliamo deve avere un senso per chi ascolta e deve quindi rispettare le regole della logica. Se comunichiamo informazioni scientifiche o siamo alla ricerca di nuova conoscenza che scaturisce da altre conoscenze dobbiamo seguire i metodi e le leggi della logica.
La logica costituisce quindi il fondamento sul quale si basano sia il linguaggio che la conoscenza scientifica.