|
.. La prima applicazione, molto
nota, è proprio quella già descritta con N=5 ; in tal caso
la statistica, che si usa indicare con LT, ci dice quanti dei
5 numeri estratti ad una certa data ci attendiamo che siano
ancora in piedi al ritardo R. Una seconda applicazione si
ottiene considerando globalmente le 10 ruote assumendo quindi
per N il valore 50 (eventuali numeri comuni a due o più ruote
vanno considerati indipendenti fra loro). In questo caso la
statistica è convenzionalmente indicata con NT
e ci dice quanti dei 50 numeri estratti ad una
certa data saranno teoricamente ancora in piedi al ritardo R
sull’insieme delle 10 colonne dei ritardi. Una terza
applicazione pone N=10 ; in questo caso la statistica,
indicata con PT, si
riferisce ancora alle dieci ruote ma ipotizza che si sia
selezionata preventivamente una tra le cinque posizioni di
estrazione dei numeri su una ruota (primo estratto, secondo
estratto ecc. ). Se si sceglie ad esempio la prima posizione,
PT ci dice quanti dei 10 numeri in prima posizione ad una
certa data sono ancora in piedi, secondo la teoria, al ritardo
R. In tutti questi casi N
è un semplice fattore moltiplicativo. L’andamento temporale
(al crescere cioè del ritardo) è fissato esclusivamente dal
fattore q(R-1). Alle
statistiche teoriche appena illustrate, il cui nome contiene
una T come seconda
lettera, corrispondono quelle reali, rilevate dalla situazione
estrazionale attuale, cioè dal tabellone dei ritardi. La
determinazione delle statistiche reali, che vengono indicate
col simbolo che si ottiene sostituendo la lettera T con una R
(reale), è facilissima. Così LR
si ottiene semplicemente contando nella colonna dei ritardi di
una ruota quanti dei 5 numeri iniziali sono ancora in piedi al
ritardo R (i numeri che hanno lo stesso ritardo su una ruota
sono detti sincroni ). Per quanto riguarda NR sarà
sufficiente sommare le LR delle 10 ruote per ogni valore
costante di R (i numeri che hanno lo stesso ritardo su ruote
diverse sono detti isocroni ). Infine per quanto riguarda PR
basterà vedere quanti dei 10 numeri iniziali estratti, ad es.
in prima posizione sulle 10 ruote, sono ancora in piedi al
ritardo R (e analogamente per i numeri in seconda posizione e
così via ; i numeri che hanno la stessa posizione, allo
stesso ritardo, sono detti isotopi ). A questo punto si
applica una metodologia per confrontare la situazione reale
con quella teorica, valutarne gli scostamenti, in modo da
ricavarne un indice di aspettabilità. La metodologia (cfr.
Tosco da Montalbano e Leontino Gorgia "IL LOTTO : Nuove e
avanzate metodologie previsionali" - Gino Pinna Editore,
1994) consente di esprimere attraverso un numero compreso fra
0 e 1, detto "aspettabilità" parziale (Apz) la
deviazione fra una qualsiasi statistica reale e la
corrispondente statistica teorica. Se il valore di Apz risulta
circa 0.5 non vi è praticamente deviazione fra caso pratico e
teoria ; se il valore risulta maggiore di 0,5 il caso pratico
mostra un eccesso rispetto al caso teorico ; in tal caso si
dice che i numeri interessati (che partecipano alla
fluttuazione) mostrano una "alta aspettabilità" ;
il viceversa è detto se il valore dell’Apz risulta
inferiore a 0,5. Il valore di una Apz non è una probabilità
: questa rimane costante ad ogni estrazione. Tuttavia il
valore di una certa Apz, misurando la deviazione fra una
statistica reale e la corrispondente statistica teorica, può
essere assunto come il grado di fiducia che si può investire
nella prossima uscita di certi numeri (partecipanti ad una
fluttuazione) esclusivamente per ragioni di riequilibrio
statistico. Poiché vi possono essere tante aspettabiltà, vi
saranno tante Apz quante sono le statistiche che si possono
utilizzare. Il simbolo specifico di una Apz è dato da una A
seguita dalla lettera maiuscola che caratterizza la
statistica. La formula da applicare, denominando con XR
la generica statistica reale, è data da :
AX = XR/(XR+XT)
per cui sono definibili immediatamente tre Apz, da quanto
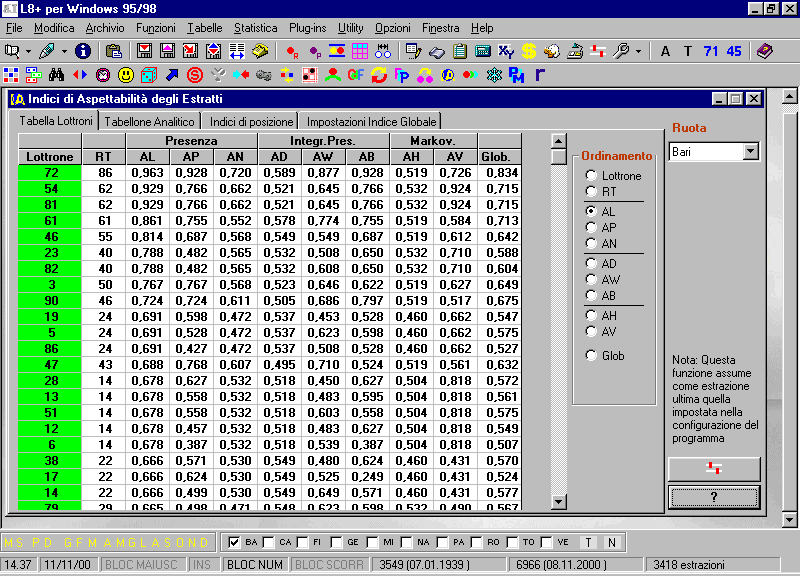
esposto in precedenza : AL, AP e AN.
|
