Andamento
degli estratti
| Fascia di Ritardo |
Estratti teorici secondo il "Fisico" |
Numeri residui |
Estratti teorici secondo la "Legge del Terzo" |
Numeri residui |
| 18 |
55,9402397878027 |
34,05976021 |
60,0000000000000 |
30,00000000 |
| 36 |
77,8264546190676 |
12,17354538 |
80,0000000000000 |
10,00000000 |
| 54 |
85,6489650479527 |
4,35103495 |
86,6666666666667 |
3,33333333 |
| 72 |
88,4448651102423 |
1,55513489 |
88,8888888888889 |
1,11111111 |
| 90 |
89,4441679848598 |
0,55583202 |
89,6296296296296 |
0,37037037 |
| 108 |
89,8013360570266 |
0,19866394 |
89,8765432098765 |
0,12345679 |
Secondo voi è possibile stabilire quanti numeri
verranno estratti (o viceversa, rimarranno da estrarre) ad un dato
ritardo?
La risposta è senz'altro affermativa. Infatti, secondo la più accreditata teoria, in un arco specifico di estrazioni, è
possibile stabilire a priori quanti numeri resteranno ancora da estrarre e, di converso,
quanti ne usciranno.
In questa prima tabella abbiamo evidenziato ciò che scaturisce dalle formule di due scuole di pensiero:
· quella del FISICO
· e quella della classica " L.d.T. = LEGGE DEL TERZO".
Le risultanze di tali conteggi, dapprima discordanti, tendono, con il passare del tempo, ad equivalersi.
Ma
veniamo alla genesi di simili formulazioni. Il Fisico, partendo dal famoso
presupposto che in 18 estrazioni
dovrebbero, almeno in teoria, essere estratti tutti i 90 numeri, ha
concepito la sua formula, tenendo però conto che nella realtà, per effetto
della ripetizione estrattiva di alcuni numeri, solo una parte, dei 90 deputati
all’uscita, faranno la loro effettiva comparsa, mentre gli altri resteranno
ancora relegati nell’urna. Per dimostrare ciò, si è avvalso, nella sua concezione,
della probabilità contraria che viene convenzionalmente indicata in 17/18
elevandola alla potenza R-1 (ossia alle estrazioni di ritardo –1). In sintesi
la formula assume la seguente connotazione:
90 * (17/18) ^ (R-1)
Per
cui, in base a tale formula, alla diciottesima estrazione di ritardo, figura che
rimangono
da estrarre circa 34 numeri, alla trentaseiesima circa 12 e così via (vedi la
tabella sopra riportata).
La legge del Terzo, invece, parte dal presupposto che nell’arco di un ciclo teorico (ovvero 18 estrazioni), solo 2/3 dei numeri non ancora usciti faranno la loro comparsa, mentre il restante terzo rimarrà nell’urna. La formula, in verità molto semplice, per il primo ciclo, si può così riassumere:
90 * 1/3 = 30
Al
secondo ciclo (ossia dalla 19esima alla 36esima estrazione di ritardo),
occorrerà calcolare il terzo sui residui 30 numeri; per cui: 30 * 1/3 = 10
numeri ancora da sortire, e così via (si veda in proposito la tabella sopra
riportata).
Nella
realtà, com’è logico dedurre, succede di tutto, però, man mano che le
estrazioni si susseguono, i dati reali tendono ad uniformarsi ai valori teorici
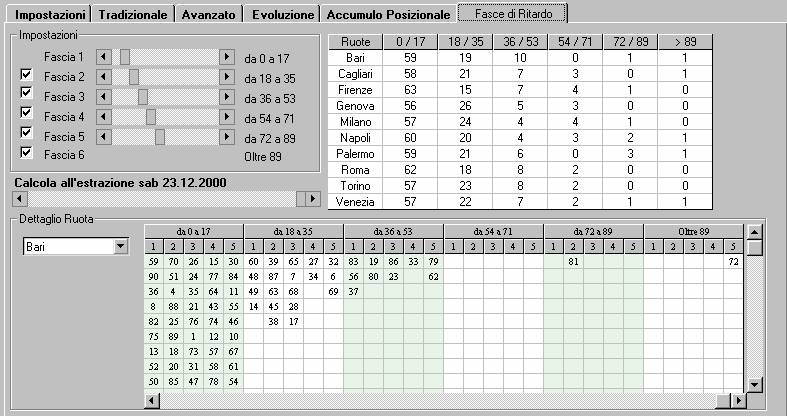
sopra espressi. Consultate in proposito la tabella riportata qui sotto, che è
la sintesi della situazione reale venutasi a creare all’estrazione del 23/12/00,
e vi renderete conto come tutte le ruote (a parte qualche minimo scarto),
tendano ad avvalorare quanto espresso dalle formule. In pratica tale tabella ci
dice, ad esempio, che a Bari nel primo ciclo, sono stati estratti 59 numeri (ne
residuano quindi 31), al secondo ciclo ne sono stati estratti ulteriori 19 (con
residuo di 12) ecc. Verificate voi stessi ruota per ruota e traetene le
eventuali conclusioni. A questo punto risulta veramente facile individuare i
numeri candidati ad essere estratti nelle prossime estrazioni. Prendiamo, per
l’appunto, i numeri che segnano un ritardo uguale o maggiore di 36 e
confrontiamone gli andamenti secondo la tabella riprodotta sopra; ebbene, se
consideriamo che alla fine del ciclo successivo (54^ estrazione) rimarranno da
estrarre, mediamente, solo 3 o 4 numeri, inseguire per ambata, quindi, i 10 o
12 numeri che risultano non estratti alla 36^ estrazione, è una vera manna dal
cielo. Tutto ciò perché, in base a quanto esprimono questi dati teorici (che
poi generalmente si riflettono anche nella realtà), dovrebbero uscire almeno 7
o 8 ambate che, se seguite opportunamente, magari adottando la “tecnica degli
insiemi”, saranno foriere di grandi soddisfazioni.
![]() Immagine tratta dal programma L8+ per Windows v.4.0.30 © 2000-2001 F.Perona - M.Romano
Immagine tratta dal programma L8+ per Windows v.4.0.30 © 2000-2001 F.Perona - M.Romano