Ci sono diversi modi per risolvere un sudoku, sono comunque tutti sistemi basati sulla logica e sulla pazienza, quello che vado ed esporvi è fra tutti il più semplice anche se alle prime può apparire più laborioso.

Si può adottare questo metodo sia sul pc (sullo stesso foglio excell che vi mando) sia su carta, ma essendo necessario cancellare dei numeri se si fa su carta è meglio usare matita e gomma.

Esistono naturalmente programmini per risolvere qualsiasi sudoku anche quelli a 16 cifre, e se uno è bravo a usare il pc se li può creare da se anche in excell, ma così che gusto ci sarebbe?

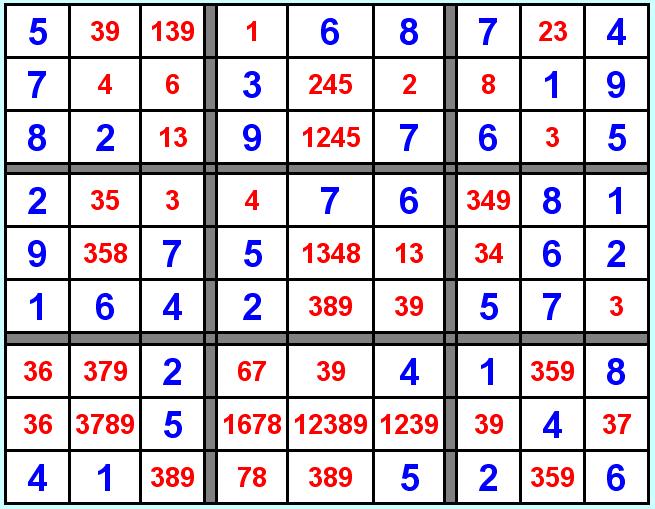
Il metodo consiste nell'inserire in ogni casella i numeri mancanti, escludendo quelli già presenti all'interno del riquadro, sulla stessa riga e sulla stessa colonna.

Come si può vedere dall'esempio (ne ho scelto uno facile facile), non ho escluso i numeri che ho trovato fissi mentre inserivo le varie possibilità (quelli soli soletti scritti in rosso, per esempio nella seconda riga del secondo quadrante potevo fare a meno di scrivere il 2 nella casella centrale 245 perchè il 2 è rimasto fisso nella casella di destra), consiglio di farlo comunque almeno finchè non avrete la padronanza del gioco.

A questo punto specie per i principianti consiglio di salvare il risultato in un file provvisorio, perchè se dopo le eliminazioni saltasse fuori qualche errore dovreste ricominciare d'accapo con l'operazione più noiosa.

Procediamo adesso ad eliminare dalle caselle i nuovi numeri fissi che abbiamo trovato, e se troviamo ulterioriori numeri fissi continuiamo nell'operazione.

Dall'esempio preso, essendo facile facile, vedremo che un tassello alla volta alla fine il sudoku è risolto come qui a lato.

Ma chiaramente nei sudoku più difficili, essendoci meno numeri fissi di partenza, ci saranno di conseguenza più possibilità di inserimento nelle varie caselle, e finita questa operazione ci potremmo trovare in situazioni di stallo da dare capocciate nel muro.

Andiamo quindi a vedere qualche trucchetto o meglio qualche ragionamento che ci aiuti.

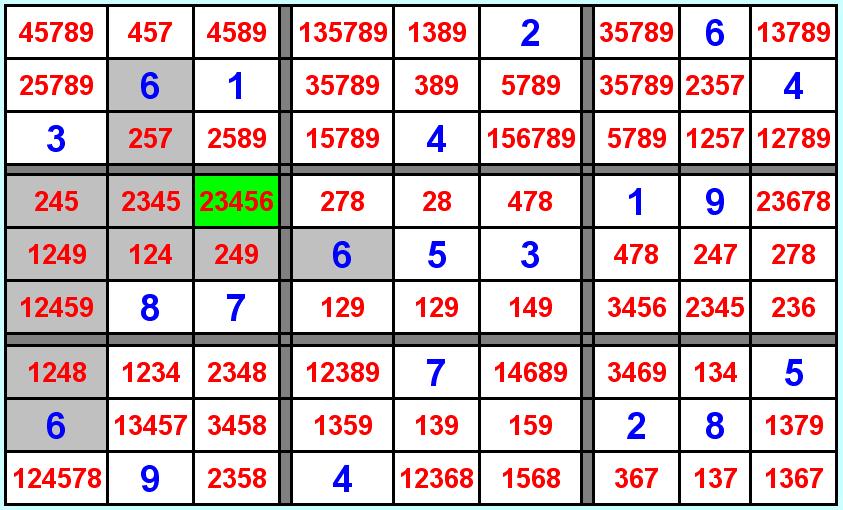
Ho preso ad esempio il sudoku N°4. quella che vedete a fianco è la situazione che vi si presenta quando avete inserito tutto le possibilità, tragica.

Una volta presa confidenza con i metodi questa deduzione ci salterà all'occhio subito, guardando nel primo  quadrante della fila centrale, ci rendiamo conto che il 6 può essere collocato nella sola terza casella (quella a sfondo verde) le altre posizioni sono infatti precluse dai sei già posizionati nello schema

Andremo quindi a fissare il 6 nella casella verde e a cancellare tutti i sei nella stessa riga e colonna, per sfortuna ne abbiamo solo uno nell'ultima casella a destra della riga ma non importa, vedrete infatti che nel quadrante dove abbiamo fissato il 6 eliminando 2345, ci rimane un unico 3 nella seconda casella della prima riga, fissiamo quindi pure il 3 ed andiamo ad eliminare tutti i 3 sulla stessa riga e colonna, questa volta ce ne sono un pò di più.

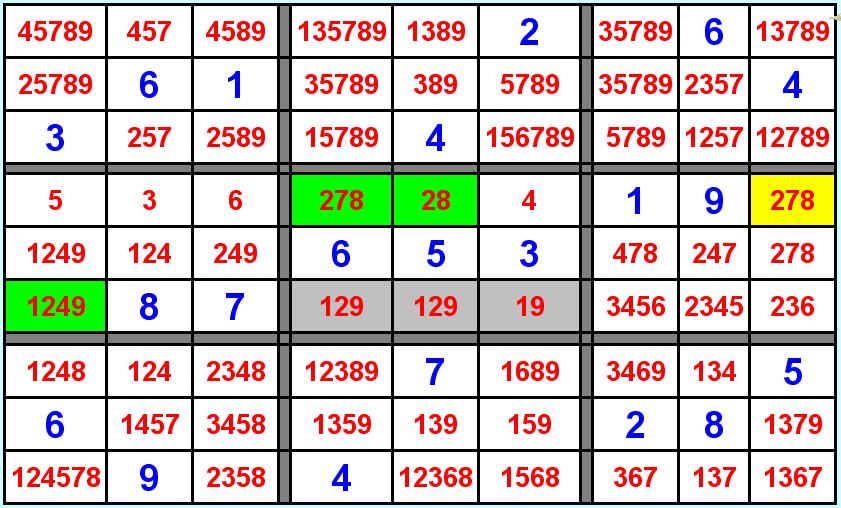
Adesso osservate le tre caselle a sfondo grigio sulla quarta riga dello schema, 278  28  e 278 il che vuol dire che in quelle tre caselle potranno esserci solo 2 7 e 8, il che vuol dire che questi tre numeri non possono trovarsi in altre caselle della stessa riga (sarebbe stato lo stesso ragionamento in una colonna o in quadrante).

Andremo quindi ad eliminare tutti 2 i 7 e gli 8 della riga per cui si fissa il 4 nella casella verde, elimineremo anche il due della prima casella, e così pure il 4 della prima casella avendolo fissato nella casella verde, di conseguenza nella prima casella rimarrà fissato il 5, provvediamo quindi a ripulire i 4 e i 5 dai rispettivi quadranti, righe e colonne e vediamo cosa succede.

Succede proprio una cosa interessante, le tre caselle a sfondo grigio sulla terza riga del quadrante centrale, contengono i soli numeri 1 2 e 9, perciò, per lo stesso principio del passaggio precedente andremo ad eliminire tutti gli 1, i 2 e i 9 contenuti nelle caselle del quadrante e della riga, in particolar modo vedremo che nelle caselle a sfondo verde del quadrante si fissano il 7 e l'8, e di conseguenza nella casella a sfondo giallo si fissa il 2, mentre nella prima casella della riga (a sfondo verde) si fissa il 4.

Adesso non ci resta che ripulire lo schema dai numeri che vengono esclusi dai nuovi numeri fissi, perciò via tutti i quattro dalla prima colonna, dalla sesta riga e dal quarto quadrante, via i 7 dalla quarta colonna, dalla quarta riga e dal quinto quadrante, via gli 8 dalla quinta colonna, dalla quarta riga e dal quinto quadrante, e via i 2 dalla nona colonna dalla quarta riga e dal sesto quadrante, ora la quarta riga è completamente fissa.

Ed ora questa regoletta dovreste averla capita.

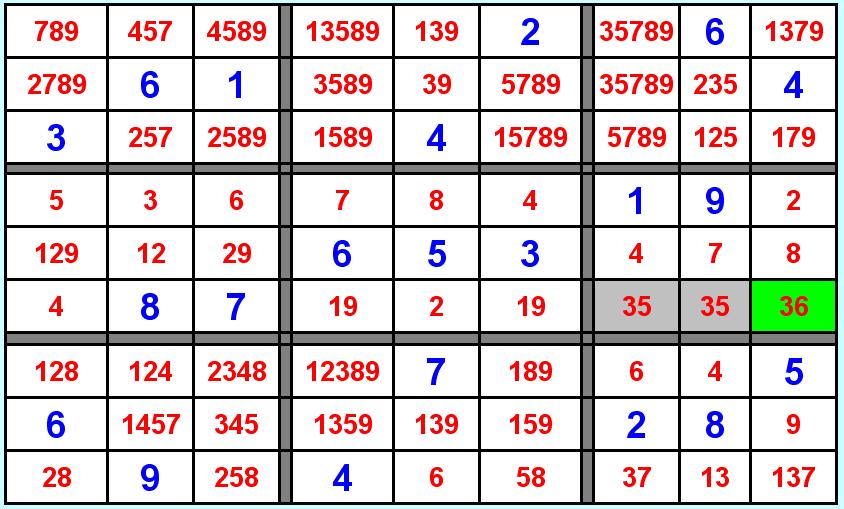
Dopo aver ripetuto le due precedenti regolette per un pò di volte ci si presenta l'opportunità di applicare un nuovo ragionamento anche se nel caso specifico poco produttivo.

Esaminiamo il sesto qudrante, ci accorgiamo che le due celle in grigio, contengono 35, questo significa che necessariamente saranna o 3 o 5 per cui potremo procedere ad eliminare tutti i 3 e i 5 all'interno del quadrante, in questo caso essendo le due celle sulla stessa riga anche dalla riga, nel caso specifico andremo quindi a fissare il 6 nella casella a sfondo verde.

Il ragionamento funziona anche in senso inverso, se cioè i numeri 3 e 5 (o qualsiasi altra coppia o terna) si trovano esclusivamente in 2 (3 per la terna) caselle dello stesso quadrante, della stessa riga o colonna, tutti gli altri numeri insieme presenti su quelle 2 o 3 caselle vanno eliminati e le caselle diventano una coppia (o una terna).

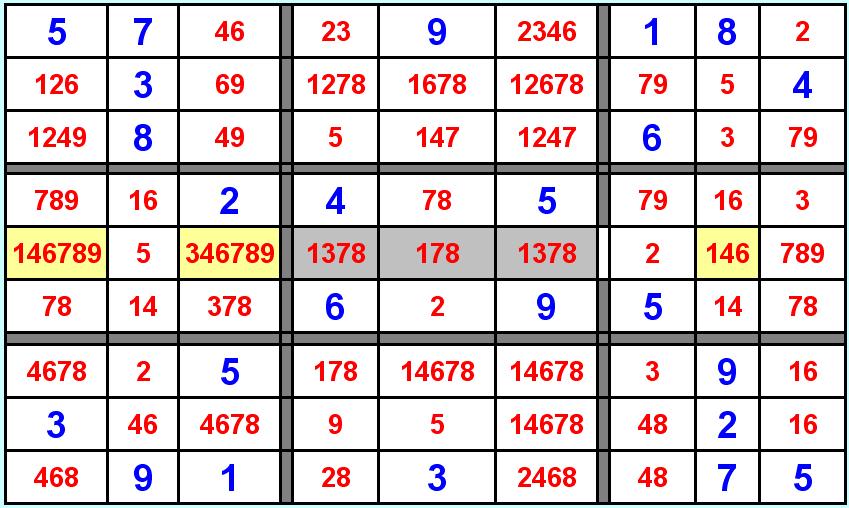
Prendiamo ad esempio il SUDOKU N°4 dopo aver ripetuto le due precedenti regolette per un pò di volte ci si presenta l'opportunità di applicare un nuovo ragionamento.

Esaminiamo il quadrante centrale, ci accorgiamo che 1 e 3 si trovano solo sulle tre caselle della quinta riga, questo significa che nel quadrante 1 e 3 devono necessariamente trovarsi sulla quinta riga, per cui andremo ad eliminare tutti gli altri 1 e 3 della riga stessa (celle a sfondo giallo).

Il ragionamento funziona anche in senso inverso, se cioè i numeri 1 e 3 (o qualsiasi altra coppia o terna o anche un numero soltanto) si trovano su una riga o colonna all'interno di un solo quadrante, questi numeri andranno eliminati dal resto del.