|
Domanda
|
| 1) Il teorema di Pitagora si può
applicare |
| a un triangolo equilatero |
| a un rettangolo |
| a ogni triangolo |
| a un triangolo isoscele con un angolo retto |
|
2) In un triangolo
rettangolo il quadrato costruito su ... è equivalente alla ... del
quadrato costruito su ... con il quadrato costruito sull'altro cateto.
Quali sono nell'ordine le
parole mancanti? |
| ipotenusa, differenza, cateto |
| ipotenusa, somma, ipotenusa |
| cateto, somma, cateto |
| cateto, differenza, ipotenusa |
| 3) Di un triangolo rettangolo si
conosce solo la misura dell'ipotenusa; quale teorema si può applicare per
calcolare i cateti? |
| Il teorema di Pitagora |
| Il primo teorema di Euclide |
| Il secondo teorema di Euclide |
| Nessuno dei tre teoremi |
| 4) I lati
di un triangolo misurano 3cm, 4cm, 5cm. Che tipo di triangolo
è? |
| rettangolo |
| isoscele |
| equilatero |
| non è un triangolo |
| 5) La misura della diagonale di un
rettangolo è uguale alla |
| radice quadrata della somma della base con
l'altezza |
| radice quadrata del prodotto della base per l'altezza
|
| somma del quadrato della base con il quadrato
dell'altezza |
| radice quadrata della somma del quadrato della base con
il quadrato dell'altezza |
|
6)Nel trapezio isoscele della figura, conoscendo la misura
del lato obliquo AD e la misura della sua proiezione AH sul lato
AB, |
 |
| posso calcolare la misura dell'altezza DH applicando il
teorema di Pitagora al triangolo ADB |
| posso calcolare la misura dell'altezza DH applicando il
teorema di Pitagora al triangolo ADH |
| posso calcolare la misura dell'altezza DH applicando il
teorema di Pitagora al triangoloADCB |
| non posso calcolare l'altezza |
| 7) In un triangolo rettangolo i
due cateti misurano rispettivamente 4cm e 3cm. Quanto misura
l'ipotenusa? |
| 5 cm |
| 25 cm |
| radice di 5 cm |
| 25 cm2 |
| 8) Il lato di un quadrato misura
1cm. Quanto misura la sua diagonale? |
| radice di 2 |
| 2 |
| radice di 4 |
| radice di 1 |
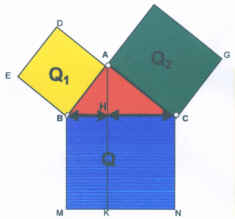
| 9)Nella figura il quadrato Q si scompone in
due rettangoli |
 |
| equivalenti |
| equivalenti a Q1 |
| equivalenti a Q2 |
| aventi la stessa altezza |
| 10) Nella figura precedente il
quadrato Q1 è equivalente |
| al triangolo ABC |
| al triangolo ABH |
| al rettangolo MKHB |
| al quadrato Q2 |

