|
Domanda
|
| 1)Un triangolo rettangolo è un
triangolo che ha |
| due lati uguali |
| gli angoli retti |
| due lati perpendicolari |
| due angoli ottusi e uno retto |
| 2) Due figure sono equivalenti se
hanno |
| la stessa forma |
| la stessa area |
| le stesse dimensioni |
| gli angoli uguali |
| 3) La proiezione del cateto AB
sull'ipotenusa è |
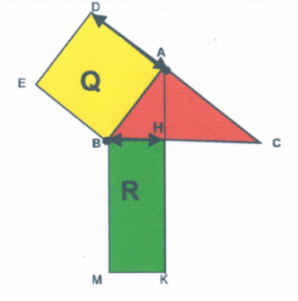 |
| H |
| AH |
| BC |
| BH |
| 4) Due
angoli si dicono complementari, quando |
| la loro somma dà un angolo retto |
| la loro somma dà un angolo piatto |
| la loro differenza dà un angolo retto |
| sono uguali |
| 5) Il teorema di Euclide afferma
che in un triangolo rettangolo il quadrato costruito |
| sull'ipotenusa è equivalente al rettangolo che ha per
lati il cateto e la proiezione del cateto sull'ipotenusa |
| su un cateto è equivalente al rettangolo che ha per lati
la proiezione del cateto sull'ipotenusa e l'ipotenusa. |
| su un cateto è equivalente alla differenza tra il
quadrato costruito sull'ipotenusa e quello costruito sull'altro
cateto |
| sull'altezza è equivalente al rettangolo che ha per lati
l'ipotenusa e la proiezione del cateto sull'ipotenusa. |
| 6) La distanza tra due rette
parallele è |
| la misura del segmento staccato dalle due rette su una
loro perpendicolare |
| la retta perpendicolare alle due rette date |
| la misura di un segmento che unisce due punti delle
rette |
| la distanza tra i punti medi delle rette |
| 7) Nella figura il rettangolo R è
equivalente al parallelogrammo P, perché |
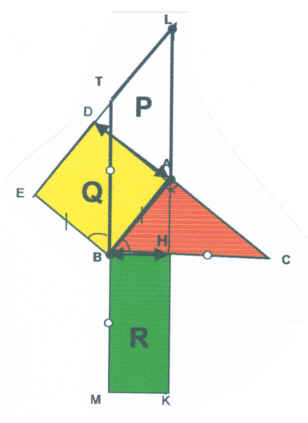 |
| Q è equivalente a R |
| hanno la stessa base e la stessa altezza |
| la misura delle basi uguali e l'altezza BH in
comune |
| la misura delle basi uguale e l'altezza AB in
comune |
| 8) Nella figura precedente P è
equivalente a Q |
| per la proprietà transitiva dell'equivalenza
|
| per la proprietà commutativa dell'equivalenza
|
| perché entrambi quadrilateri con la stessa base
AB |
| perché hanno la stessa base e la stessa altezza
|
| 9) Dalla formula AB2 =
BH · BC si
ottiene |
| BH = AB2 /BC |
| BH =
AB /BC |
| BH =
AB/BC2 |
| BH
= BC / AB2 |
| 10) Conoscendo le misure
BH =
9/5cm e BC = 5cm, calcolare l'area del triangolo ABC |
| area = 6 cm |
| area = 6 cm2 |
| area = 12 cm |
| area = 12 cm2 |

