Il paradosso EPR si basa su un fenomeno predetto dalla meccanica quantistica, conosciuto come entanglement quantistico, per mostrare che misure compiute su parti di un sistema fisico separate spazialmente possono avere in apparenza un'influenza istantanea l'una sull'altra. Questo effetto è noto come non località. Per illustrare tutto questo, consideriamo la versione semplificata dell'esperimento ideale di EPR, formulata da David Bohm. Si supponga di avere una sorgente che emette coppie di elettroni, uno dei quali viene inviato alla destinazione A, dove c'è un'osservatore di nome Claudio, e l'altro viene inviato alla destinazione B, dove c'è un osservatore di nome Lucio. Secondo la meccanica quantistica, possiamo sistemare la sorgente in modo che ciascuna coppia di elettroni emessi occupi uno stato quantistico detto singoletto di spin. Questo si può descrivere come sovrapposizione quantistica di due stati, indicati con I e II. Nello stato I, l'elettrone A ha spin parallelo all'asse z (+z) e l'elettrone B ha spin antiparallelo all'asse z (-z). Nello stato II, l'elettrone A ha spin -z e l'elettrone B ha spin +z. È quindi impossibile associare ad uno dei due elettroni nel singoletto di spin uno stato di spin definito: gli elettroni sono intrecciati. 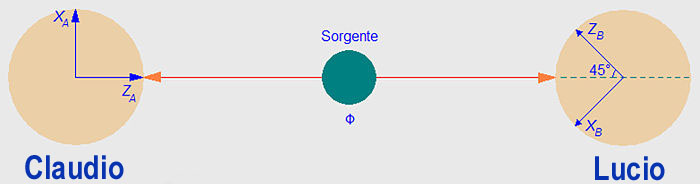 - La figura dimostra lo stato Riproposizione dell'esperimento suggerito da Einstein, Podolsky e Rosen, eseguito con elettroni. Una sorgente invia elettroni verso due osservatori, Claudio (a sinistra) e Lucio (a destra), i quali sono in grado di eseguire misure della proiezione dello spin degli elettroni lungo un asse. Claudio misura lo spin lungo l'asse z. Si può ottenere uno dei due possibili risultati: +z o -z. Supponiamo che ottenga +z. Secondo la meccanica quantistica, la funzione d'onda che descrive lo stato di singoletto dei due elettroni, collassa nello stato I (le diverse interpretazioni della meccanica quantistica dicono questo in diversi modi, ma il risultato alla fine è lo stesso). Lo stato quantistico determina le probabilità dei risultati di qualunque misura fatta sul sistema. In questo caso, se Lucio successivamente misurasse lo spin lungo l'asse z, otterrebbe -z con una probabilità del 100%. Analogamente, se Claudio misurasse -z, Lucio otterrebbe +z, sempre con una probabilità del 100%. Naturalmente non c'è niente di speciale nella scelta dell'asse z. Ad esempio, supponiamo che Claudio e Lucio decidano di misurare lo spin lungo l'asse x. Secondo la meccanica quantistica, lo stato di singoletto di spin può essere espresso adeguatamente come sovrapposizione di stati di spin lungo la direzione x, stati che chiameremo Ia e IIa. Nello stato Ia l'elettrone di Claudio ha spin +x, quello di Lucio ha spin -x, invece nello stato IIa l'elettrone di Claudio ha spin -x, quello di Lucio ha spin +x. Quindi, se Claudio misura +x, il sistema collassa in Ia, e Lucio misurerà -x, con probabilità del 100%; se Claudio misura -x, il sistema collassa in IIa e Lucio misurerà +x, con probabilità del 100%. In meccanica quantistica, la proiezione dello spin lungo x e quella lungo z sono quantità osservabili tra loro incompatibili, per cui gli operatori associati non commutano, cioè uno stato quantistico non può possedere valori definiti per entrambe le variabili (principio di indeterminazione). Supponiamo che Claudio misuri lo spin lungo z e ottenga +z, in modo che il sistema collassi nello stato I. Ora, invece di misurare lo spin lungo z, Lucio misura lo spin lungo x : secondo la meccanica quantistica, c'è il 50% di probabilità che egli ottenga +x e il 50% di probabilità che ottenga -x. Inoltre, è impossibile predire quale sarà il risultato fino a quando Lucio non esegue la misura. È bene sottolineare che, benché si sia usato lo spin come esempio, si possono considerare molte altre quantità fisiche (osservabili), tra loro entangled. L'articolo originale di EPR, per esempio, usava l'impulso come quantità osservabile. Gli esperimenti odierni usano spesso la polarizzazione dei fotoni, perché più facile da preparare e quindi misurare. Introdurremo ora due concetti usati da Einstein, Podolsky e Rosen fondamentali per il loro attacco alla meccanica quantistica: il realismo o oggettivismo e la completezza di una teoria fisica. Se il valore di ogni quantità fisica di un sistema può essere predetto con assoluta certezza prima di fare una misura o prima di intervenire in qualche modo sul sistema medesimo, allora tale quantità esprime un elemento fisico di realtà. Notare che l'opposto, cioè la negazione dell'affermazione precedente, non porta necessariamente ad un assunto vero; possono esserci altre espressioni di elementi fisici di realtà, ma questo fatto non ha influenza sul resto dell'argomentazione. In aggiunta, EPR definisce una teoria fisica completa come una teoria in cui ogni elemento fisico di realtà sia preso in considerazione. Lo scopo è mostrare, usando queste due definizioni, che la meccanica quantistica non è una teoria fisica completa. Vediamo come questi concetti si applicano all'esperimento pensato di cui sopra. Supponiamo che Claudio decida di misurare lo spin lungo z (lo chiameremo z-spin). Dopo che Claudio esegue la misura, lo z-spin dell'elettrone di Lucio è noto, quindi è un elemento fisico di realtà. Analogamente, se Claudio decidesse di misurare lo spin lungo x, l'x-spin di Lucio sarebbe un elemento fisico di realtà dopo la sua misura. Uno stato quantistico non può possedere contemporaneamente un valore definito per lo x-spin e lo z-spin . Se la meccanica quantistica è una teoria fisica completa nel senso dato sopra, l'x-spin e lo z-spin non possono essere elementi fisici di realtà allo stesso tempo. Questo significa che la decisione di Claudio di eseguire la misura lungo l'asse x o lungo l'asse z ha un effetto istantaneo sugli elementi fisici di realtà nel luogo in cui si trova Lucio ad operare con le sue misure. Tuttavia, questa è una violazione del principio di località o principio di separazione. Il principio di località afferma che processi fisici che avvengono in un posto non possono avere effetto immediato su elementi fisici di realtà in un altro luogo, separato dal primo. A prima vista, questa appare un'assunzione ragionevole, infatti a livello macroscopico è ragionevole, in quanto è una conseguenza della relatività speciale, la quale afferma che le informazioni non si possono mai trasmettere a una velocità maggiore di quella della luce senza violare la causalità. Generalmente si crede che ogni teoria che violi la causalità sia anche internamente inconsistente, e quindi del tutto insoddisfacente. Si trova che la meccanica quantistica viola il principio di località senza violare la causalità. La causalità è preservata perché non c'è alcun modo per Claudio di trasmettere un messaggio (cioè informazioni) a Lucio variando l'asse lungo cui fa la misura. Qualunque asse lei scelga, ha sempre il 50% di probabilità di ottenere "+" e il 50% di ottenere "-", del tutto a caso; secondo la meccanica quantistica, è del tutto impossibile per lei influire sul risultato che otterrà. Inoltre, Lucio può fare la sua misura una sola volta, in quanto il collasso della funzione d'onda provocato dalla misura perturba in maniera irreversibile lo stato misurato: c'è una proprietà basilare della meccanica quantistica, nota come "no cloning theorem", che rende impossibile per l'osservatore fare, diciamo, un milione di copie dell'elettrone che riceve, eseguire misure sullo spin di ciascuno e poi analizzare la distribuzione statistica dei risultati. Quindi, nell'unica misura che gli è permesso fare, c'è il 50% di probabilità di ottenere "+" e il 50% di ottenere "-", indipendentemente dal fatto che il suo asse sia allineato o meno con quello di Claudio. Tuttavia, il principio di località si richiama fortemente all'intuizione fisica di livello macroscopico, e Einstein, Podolsky e Rosen non volevano abbandonarlo. Einstein derise le predizioni della meccanica quantistica come spaventosa azione a distanza. La conclusione che trassero fu che la meccanica quantistica non è una teoria completa. Si deve far notare che la parola località ha diversi significati in fisica. Per esempio, in teoria quantistica dei campi località significa che campi in punti diversi dello spazio non interagiscono l'uno con l'altro. Tuttavia, le teorie di campo quantistiche che sono locali in questo senso violano il principio di località come definito da EPR. Risoluzione del paradosso EPR Esistono parecchi possibili modi per risolvere il paradosso EPR. Quello ipotizzato da EPR è che la meccanica quantistica, nonostante il successo in una ampia e vasta varietà di scenari sperimentali, sia in realtà una teoria incompleta. In altre parole, esiste qualche ancora non scoperta teoria della natura rispetto alla quale la meccanica quantistica gioca il ruolo di una specie di approssimazione statistica (benché sia baciata in fronte da un successo strepitoso). A dispetto della meccanica quantistica, questa teoria più completa contiene variabili che tengono conto di tutti gli elementi fisici di realtà. Deve esistere qualche ignoto meccanismo che agisce su queste variabili che dà origine agli effetti osservati nelle osservabili quantistiche non-commutanti, vale a dire il principio di indeterminazione di Heisenberg. Tale teoria si chiama teoria delle variabili nascoste. Per illustrare questa idea, si può formulare una teoria delle variabili nascoste molto semplice per l'esperimento pensato di cui sopra. Si supponga che gli stati quantistici di spin di singoletto emessi dalla sorgente siano in realtà descrizioni approssimate dei veri stati fisici che possiedono valori definiti per lo z-spin e per l' x-spin. In questi stati veri, l'elettrone che va verso Lucio ha sempre valori di spin opposti rispetto all'elettrone che va verso Claudio, ma tali valori sono completamente random (casuali). Per esempio, la prima coppia emessa dalla sorgente può essere (+z, -x) verso Claudio e (-z, +x) verso Lucio, la coppia successiva (-z, -x) verso Claudio e (+z, +x) verso Lucio e così via. Per ciò, se l'asse della misura di Lucio è allineato con quello di Claudio, egli otterrà necessariamente l'opposto di qualunque cosa ottenga Claudio; altrimenti egli otterrà + e - con eguale probabilità. Ipotizzando di restringere le misure solo all'asse z e all'asse x, tale teoria delle variabili nascoste è sperimentalmente indistinguibile dalla teoria della meccanica quantistica. In realtà, ovviamente, c'è un numero infinito di assi lungo i quali Claudio e Lucio possono eseguire le misure, di modo che si ha un numero infinito di variabili nascoste indipendenti! Tuttavia, questo fatto non ha conseguenze gravi; questa è una formulazione molto semplicistica di una teoria delle variabili nascoste e una teoria più sofisticata sarebbe in grado di metterci una pezza. Ne risulta che la sfida legata all'idea di variabili nascoste è molto più seria. Nel 1964, John Bell ha mostrato come le predizioni della meccanica quantistica nell'esperimento pensato EPR siano in realtà leggermente differenti dalle predizioni di una classe molto vasta di teorie delle variabili nascoste. Grosso modo, la meccanica quantistica predice correlazioni statistiche molto più forti tra i risultati di misure eseguite su differenti assi di quanto non facciano le teorie delle variabili nascoste. Queste differenze, espresse adoperando relazioni di disuguaglianza note come "disuguaglianze di Bell", sono dal punto di vista di principio individuabili sperimentalmente. Per un deduzione dettagliata di questi risultati, vedere l'articolo sul teorema di Bell. In seguito alla pubblicazione dell'articolo di Bell, cominciarono ad essere approntati tutta una serie di esperimenti per saggiare le disuguaglianze di Bell. (Come detto sopra, questi esperimenti in generale trattano con misure di polarizzazione di fotoni). Tutti gli esperimenti condotti finora hanno indicato un comportamento in linea con le predizioni della meccanica quantistica standard. Tuttavia, questi fatti non chiudono il discorso in modo definitivo. Prima di tutto, il teorema di Bell non si applica a tutte le possibili teorie "realiste". È possibile costruire teorie che eludono le sue implicazioni, per cui diventano indistinguibili dalla meccanica quantistica, per quanto queste teorie siano eminentemente non locali si reputa che violi sia la causalità sia i teoremi della relatività ristretta ai sistemi inerziali. Alcuni ricercatori del campo hanno anche tentato di formulare teorie di variabili nascoste che sfruttino scappatoie in esperimenti concreti, come per esempio le assunzioni fatte nell'interpretare i dati sperimentali. Comunque, nessuno è stato finora in grado di formulare una teoria realista locale capace di riprodurre tutti i risultati della meccanica quantistica. Attualmente la maggior parte dei fisici ritiene che la meccanica quantistica sia corretta e che il paradosso EPR sia appunto solo un "paradosso" per il fatto che le intuizioni classiche (di livello macroscopico) non corrispondano alla realtà. Si possono trarre da ciò parecchie diverse conclusioni, che dipendono da quale interpretazione della meccanica quantistica si usi. Nella vecchia interpretazione di Copenhagen, prodotta da Niels Bohr, Werner Karl Heisenberg, Pascual Jordan e Max Born, si conclude che il principio di località (o di separazione) non debba valere e che avvenga effettivamente il collasso della funzione d'onda istantaneo. Nell'interpretazione a molti-Universi, di Hugh Everett III, la località è mantenuta e gli effetti delle misure sorgono dal suddividersi e ramificarsi delle "storie" o linee d'Universo degli osservatori. Il paradosso EPR ha reso più profonda la comprensione della meccanica quantistica mettendo in evidenza le caratteristiche fondamentalmente non classiche del processo di misura. Prima della pubblicazione dell'articolo di Einstein-Podolsky-Rosen, una misura era abitualmente vista come un processo fisico di perturbazione inflitto direttamente al sistema sotto misura. Per esempio, se si fosse misurata la posizione di un elettrone, immaginiamoci illuminandolo con luce, cioè con un fiotto di fotoni, l'urto dei fotoni con l'elettrone, necessario per illuminarlo e "vedere" dov'è, avrebbe così disturbato lo stato quantomeccanico dell'elettrone, per esempio, modificandone la velocità, producendo così incertezza sulla velocità, esemplificando così l'indeterminazione quantomeccanica su posizione e velocità, grandezze meccaniche necessarie a determinare l'evoluzione dello stato meccanico, grandezze coniugate. Tali spiegazioni, che ancora si incontrano in esposizioni non specialistiche, scolastiche e divulgative della meccanica quantistica, sono completamente demistificate dall'analisi di Einstein-Podolsky-Rosen, che mostra chiaramente come possa effettuarsi una "misura" su una particella senza disturbarla direttamente, eseguendo una misura su un'altra particella distante, ma entangled (intrecciata) con la prima. La Meccanica quantistica non e' solo "un modo di pensare " ma sono state sviluppate tecnologie che si basano sull'entanglement quantistico (intreccio di stati quantistici). Adesempio nella crittografia quantistica, si usano particelle entangled per trasmettere segnali che non possono essere intercettati senza lasciare traccia dell'intercettazione avvenuta. Cosi come nella computazione quantistica, si usano stati quantistici intrecciati (entangled) per eseguire calcoli in parallelo, che permettono elaborazioni con velocità che non sarebberero possibile con i computer classici. Esiste poi una spiegazione che riguarda gli universi multipli molto più complicata, per quanto abbastanza verosimile. Essa stabilisce che ogni volta che qualcosa è incerto, l'"Albero dell'Universo" ( come è chiamato il fenomeno di tutte le ramificazioni possibili di eventi al pari di un'albero genealogico ) produce un nuovo ramo. Ciascuna ramificazione, appena prodotta, è un diverso universo simile al precedente. Ogni possibilità è un qualcosa che capita da qualche parte. A causa della grande astrattezza di questi concetti verrà affrontata in seguito con maggior dettaglio alla luce di nuove scoperte o intuizioni. Purtroppo a causa della morte del prof.Lucio Ossino non sara' possibile chiederci spiegazioni su questo argomento. |