Merge sort

Dividi e conquista		Analisi
Merge	Merge Sort	Merge vs. quick
Esempio		Listato

Dividi e conquista

L'algoritmo detto mergesort usa il paradigma del "dividi e conquista". Questa tecnica, usata anche nel quicksort, consiste in tre passaggi fondamentali:

Dividi il problema in sottoproblemi di uguale grandezza;
Risolvi (conquista) i sottoproblemi più piccoli ricorsivamente;
Combina i risultati per risolvere il problema principale.

In particolare per ordinare un array A[p..r] con il mergesort agiremo così:

Dividi: troviamo q, elemento a metà dell'array;
Conquista: Si fa la stessa cosa ricorsivamente in A[p..q] e A[q + 1..r];
Combina: Si fondono (merge) i sottoarray ordinati per ottenere l'array ordinato
A[p..r].

Merge

L'operazione di merge (ultimo passaggio) combina due sottosequenze ordinate per produrre una singola sequenza ordinata. Questa ripetutamente compara i primi elementi in testa alle due sottosequenze e mette in output il più piccolo valore finchè non rimane nessun elemento.
Se la scansione di uno dei vettori è arrivata all'ultima componente, si copiano i rimanenti elementi dell'altro nel vettore di output.
Il merge ha complessità lineare: infatti, se due sottoarray hanno ciascuno n componenti, abbiamo 2*n confronti (nel caso peggiore) e altrettante copie, quindi time(n) = 2*n+2*n = 4*n = O(n).

Esempio:

Mergesort è usato qui per la sequenza 6,2,9,5. Le due fasi di divisione spezzano la sequenza di input; le due fasi di merge combinano le sottosequenze ordinate generate nella precedente fase.

Analisi

Il mergesort gira nel caso peggiore con complessità rispetto al tempo O(n log₂ n). I fattori costanti non sono buoni, così non si usa mergesort per piccoli array. Siccome la funzione merge fa copie dei sottoarray, non opera in-place. Mergesort si affida pesantemente alla funzione di merge che ha complessità lineare rispetto al tempo.
Passiamo ora ai dettagli dell'analisi. Il numero di attivazioni della procedura merge-sort dipende dal numero di componenti del vettore da ordinare.
Per una analisi del merge sort è conveniente disegnare un albero per rappresentare le chiamate ricorsive.

Per semplicità, consideriamo un vettore iniziale che abbia n elementi, con n potenza di 2 (n=2^k). [ k = log₂n ]. Ecco una tabella riassuntiva delle attivazioni:

Livello	Attivazioni
(1)	1 attivazione su un vettore di n (=2^k) componenti
(2)	2 attivazioni su 2 vettori di n/2 (=2^k-1) componenti
(3)	4 attivazioni su 4 vettori di n/4 (=2^k-2) componenti
...
(i)	2^i-1 attivazioni su 2^i-1 vettori di n/(2^i-1) (=2^k-i+1) elementi;
...
log₂n+1=k+1	2^k (=n) attivazioni su 2^k vettori di 1 componente.

Attivazioni di mergesort

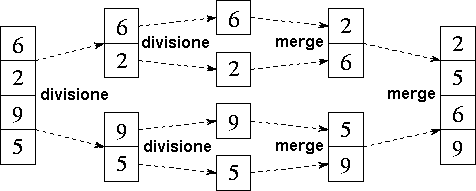
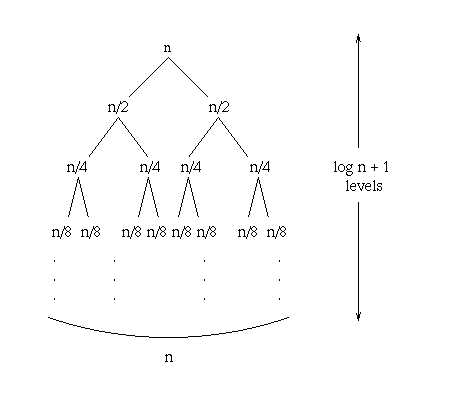
1 + 2 + 4 + ... + 2^k = 2^k+1 - 1 = 2^(log₂n+1) - 1 = 2 x 2^(log₂n) - 1 = 2n - 1 = O(n)

Operazioni di confronto

^h-1

merge

^h-1

time(n) = 2*n*k = O(n*log₂n)

Morale:

Costo_merge = n + O(n*log₂n) = O(n*log₂n)

In teoria è il "migliore" algoritmo di ordinamento (abbiamo assunto però nullo il costo di attivazione di una procedura).

Il problema dell'ordinamento di n elementi ha delimitazione inferiore W(n*log₂n).

Breve confronto con il quicksort

Intuitivamente, il quicksort "vorrebbe" suddividere a ogni passo il vettore in due sotto-vettori "circa uguali".
Come merge-sort, suddivide il vettore in due sotto-vettori, delimitati da un elemento "limite" (pivot).
Ma, mentre il merge sort si assicura questa proprietà (spezzando il vettore a metà), il quicksort ci spera soltanto: ottiene lo scopo se il pivot è "ben scelto", ma negli altri casi, funzionerà "peggio".
Queste considerazioni ci inducono a pensare che il quicksort riesca al più a emulare il merge sort, quando ha fortuna; ma senza riuscire a eguagliarlo in tutti i casi.