 Dalla costruzione verifichiamo che
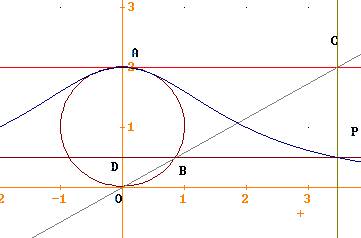
il luogo dei punti P è quello disegnato in figura(versiera di Agnesi) ;
qualsiasi retta passante per O verifica le condizioni richieste, ad eccezione
della retta orizzontale, parallela alla retta t.
Dalla costruzione verifichiamo che
il luogo dei punti P è quello disegnato in figura(versiera di Agnesi) ;
qualsiasi retta passante per O verifica le condizioni richieste, ad eccezione
della retta orizzontale, parallela alla retta t. ESAME DI STATO 2003 matematica pni. Svolgimento e soluzioni.
PROBLEMA
1
Nel
piano sono dati: il cerchio g di diametro OA = a, la retta t tangente a g
in A, una retta r passante
per
O, il punto B, ulteriore intersezione di r con g, il punto C intersezione di r
con t.
La
parallela per B a t e la perpendicolare per C a t s’intersecano in P.
Al variare di r, P descrive il
luogo
geometrico G noto con il nome di versiera di Agnesi [da Maria
Gaetana Agnesi, matematica
milanese,
(1718-1799)].
 Dalla costruzione verifichiamo che
il luogo dei punti P è quello disegnato in figura(versiera di Agnesi) ;
qualsiasi retta passante per O verifica le condizioni richieste, ad eccezione
della retta orizzontale, parallela alla retta t.
Dalla costruzione verifichiamo che
il luogo dei punti P è quello disegnato in figura(versiera di Agnesi) ;
qualsiasi retta passante per O verifica le condizioni richieste, ad eccezione
della retta orizzontale, parallela alla retta t.
(nel
grafico, a titolo di esempio, è stato preso a = 2 ma deve comunque essere >
0 trattandosi di un diametro).
1.
Si provi che valgono le seguenti proporzioni:
OD : DB = OA : DP
la prima proporzione deriva dalla similitudine dei triangoli
ODB e OAC, entrambi rettangoli e conl’angolo in O in comune e osservando che
DP e AC sono congruenti (lati opposti del rettangolo ACPB)
OC
: DP = DP : BC ove
D è la proiezione ortogonale di B su OA;
La
seconda proporzione deriva dal teorema della tangente e della secante (confronta
testo di geometria) per cui la tangente (AC)
è media proporzionale tra l’intera secante (CO) e la parte esterna (BC)
e osservando, anche in questo caso che DP e AC sono congruenti
2.
Si verifichi che, con una opportuna scelta del sistema di coordinate cartesiane
ortogonali e
monometriche Oxy, l’equazione cartesiana di G è:
![]() la
scelta del sistema è quella indicata in figura perché la funzione tende a O
per x che tende a infinito suggerisce che che corrisponda alla situazione nella
quale la retta OB non interseca la retta t (mentre inceve per x = 0 il valore èproprio
a) . La costruzione si basa sulla prima proporzione dove OD= y , DB =
la
scelta del sistema è quella indicata in figura perché la funzione tende a O
per x che tende a infinito suggerisce che che corrisponda alla situazione nella
quale la retta OB non interseca la retta t (mentre inceve per x = 0 il valore èproprio
a) . La costruzione si basa sulla prima proporzione dove OD= y , DB =
![]() OA = a , DP =
OA = a , DP =
![]() da cui
da cui
![]()
![]() possiamo dividere per y in quanto
diverso da zero non essendo possibile che l’ordinata del punto P sia 0,
infatti sarà sempre 0<y<=1
possiamo dividere per y in quanto
diverso da zero non essendo possibile che l’ordinata del punto P sia 0,
infatti sarà sempre 0<y<=1
3. Si tracci il grafico di G e si provi che l’area
compresa fra G e il suo asintoto è quattro volte quella
del cerchio g. lo
studio della funzione è semplice. La funzione è pari
infatti f(-x)= f(x), come suggerisce anche il problema (simmetria
rispetto al diametro OA che diventa simmetria rispetto all’asse y) Il campo di
esistenza è per tutto il campo reale, la funzione passa per (0,a), il segno è
sempre positivo; i limiti per x che tende a infinito tendono a 0; la derivata è
![]() , si annulla in x = 0 è positiva
per x<0 e negativa per x>0 quindi x = 0 è un punto di massimo e vale
ovviamente a. La derivata seconda è
, si annulla in x = 0 è positiva
per x<0 e negativa per x>0 quindi x = 0 è un punto di massimo e vale
ovviamente a. La derivata seconda è
![]() , si annulla per
, si annulla per
![]() , internamente a questi valori è negativa quindi la concavità è verso il
basso, esternamente è positiva quindi la concavità è verso l’alto. I flessi
hanno coordinate
, internamente a questi valori è negativa quindi la concavità è verso il
basso, esternamente è positiva quindi la concavità è verso l’alto. I flessi
hanno coordinate
![]() . L’area è data, sfruttando la parità, da
. L’area è data, sfruttando la parità, da
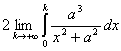 . L’int.indefinito
. L’int.indefinito
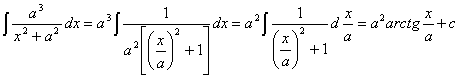 quindi
quindi
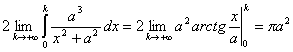 e poichè l’area del cerchio di
raggio a/2 vale
e poichè l’area del cerchio di
raggio a/2 vale
![]() l’asserto richiesto è
dimostrato.
l’asserto richiesto è
dimostrato.
PROBLEMA
2
Sia
![]() con a,b,c numeri reali. Si determinino a,b,c in modo che:
con a,b,c numeri reali. Si determinino a,b,c in modo che:
1.
la funzione f sia pari;
2.
f(0)=2;
3.
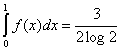
la prima condizione diventa
![]()
la seconda condizione diventa semplicemente sostituendo
la terza condizione
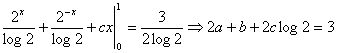
risolvendo il sistema a tre equazioni e tre incognite a = 1,
b =1 , c = 0
Si
studi la funzione g ottenuta sostituendo ad a,b,c i valori così
determinati e se ne disegni il
grafico
G.
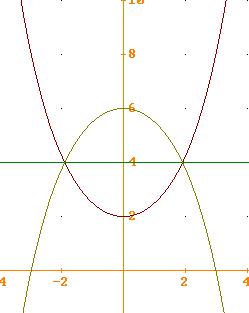 la funzione è
la funzione è
![]() , esiste per ogni x reale, è
sempre positiva perché somma di esponenziali, la derivata è
, esiste per ogni x reale, è
sempre positiva perché somma di esponenziali, la derivata è
![]() si annulla se x = 0, è positiva se
x>0 e negativa se x<0 quindi il punto (0,2) è il minimo.
si annulla se x = 0, è positiva se
x>0 e negativa se x<0 quindi il punto (0,2) è il minimo.
la
![]() è sempre positiva quindi la
concavità è verso l’alto.
è sempre positiva quindi la
concavità è verso l’alto.
Si consideri la retta r di equazione y=4 e si
determinino, approssimativamente, le ascisse dei punti in cui essa interseca G,
mettendo in atto un procedimento iterativo a scelta.
Per quanto le ascisse sia calcolabili esattamente: l’equazione
![]() , il testo chiede un procedimento di approssimazione numerica. In qusto caso
possiamo procedere in modo molto intuitivo controllando se g(x) è maggiore o
minore di 4. per x= 2 la g(2)>4 per g(1,6)<4. Utilizzando quindi
1,6<x<2. Utilizzando intuitivamente la bisezione, proviamo per 1,8 :
g(1,8)<4 quindi 1,8<x<2, ancora proviamo per 1,9: g(1,9)>4 quindi
1.8<x<1.9 (la soluzione
approssimata è x = 1,89996 ottenibile continuando il processo iterativo.
, il testo chiede un procedimento di approssimazione numerica. In qusto caso
possiamo procedere in modo molto intuitivo controllando se g(x) è maggiore o
minore di 4. per x= 2 la g(2)>4 per g(1,6)<4. Utilizzando quindi
1,6<x<2. Utilizzando intuitivamente la bisezione, proviamo per 1,8 :
g(1,8)<4 quindi 1,8<x<2, ancora proviamo per 1,9: g(1,9)>4 quindi
1.8<x<1.9 (la soluzione
approssimata è x = 1,89996 ottenibile continuando il processo iterativo.
Si
calcoli l’area della regione finita del piano racchiusa tra r e G.
è
data da
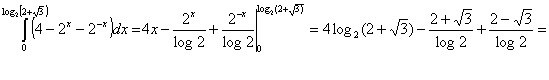
![]() . Questa è metà dell’area che è da moltiplicare per 2.
. Questa è metà dell’area che è da moltiplicare per 2.
Si
calcoli
![]()
Si determini la funzione g’ il cui grafico è
simmetrico di G rispetto alla retta r.
si ottiene
mediante la simmetria di asse y = 4 di equazioni x’=x y’=8-y
![]()
quesiti
1.
Quante partite di calcio della serie A vengono disputate complessivamente
(andata e ritorno) nel
campionato italiano a 18 squadre? sono
le disposizioni di 18 oggetti presi 2 a 2, senza ripetizione
![]()
2.
Tre scatole A, B e C contengono lampade prodotte da una certa fabbrica di cui
alcune difettose.
A
contiene 2000 lampade con il 5% di esse difettose, B ne contiene 500 con il 20%
difettose e C
ne
contiene 1000 con il 10% difettose.
Si
sceglie una scatola a caso e si estrae a caso una lampada. Quale è la
probabilità che essa sia
difettosa?
la probabilità di prendere da una delle tre scatole una
lampadina difettosa è data da
![]() dove P(A)=P(B)=P(C)=1/3 mentre le altre tre probabilità valgono 0,05
0,2 e 0,1 rispettivamente
quindi (0,05+0,2+0,1)/3= 0,12 (approssimato)
dove P(A)=P(B)=P(C)=1/3 mentre le altre tre probabilità valgono 0,05
0,2 e 0,1 rispettivamente
quindi (0,05+0,2+0,1)/3= 0,12 (approssimato)
3. Quale è la capacità massima, espressa in
centilitri, di un cono di apotema 2 dm?
indicando con x
l’altezza del cono, il raggio sarà
![]() , con x che varia tra 0 e 2 (valori estremi
= volume nullo). Il volume è
, con x che varia tra 0 e 2 (valori estremi
= volume nullo). Il volume è
![]() , la derivata è
, la derivata è
![]() il valore che annulla, nell’intervallo richiesto dal problema è
il valore che annulla, nell’intervallo richiesto dal problema è
![]() (che è facilmente verificabile
essere massimo).Il volume massimo vale in
(che è facilmente verificabile
essere massimo).Il volume massimo vale in
![]()
![]() in centilitri sarà
in centilitri sarà
![]()
4. Dare un esempio di polinomio P(x) il cui
grafico tagli la retta y=2 quattro volte.
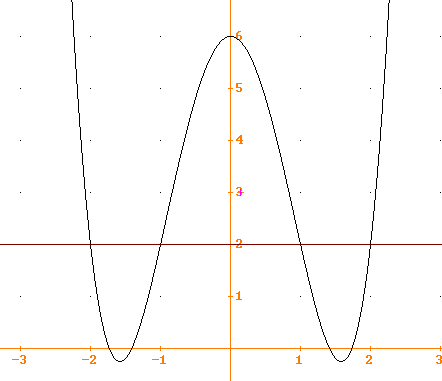
una possibilità è determinare un
polinomio che tagli quattro volte l’asse x (ad esempio
![]() che si annulla quattro
volte e traslarlo mediante x’=x e y’=y+2; si ottiene la curva cercata.
che si annulla quattro
volte e traslarlo mediante x’=x e y’=y+2; si ottiene la curva cercata.
5.
Dimostrare, usando il teorema di Rolle [da Michel Rolle,
matematico francese, (1652-1719)],
che
se l’equazione:
![]() ammette ammette radici reali,
allora fra due di esse giace almeno una radice dell’equazione:
ammette ammette radici reali,
allora fra due di esse giace almeno una radice dell’equazione:
![]() . Il
teorema di Rolle è applicabile al polinomio in quanto funzione continua e
derivabile su tutto R. I punti dove il polinomio ammette radici sono le radici
dell’equazione proposta e i valori che il polinomio
. Il
teorema di Rolle è applicabile al polinomio in quanto funzione continua e
derivabile su tutto R. I punti dove il polinomio ammette radici sono le radici
dell’equazione proposta e i valori che il polinomio
![]() per i valori della radice saranno uguale (poiché entrambi 0). allora per il
teorema, esiste almeno un punto tra le due radici dove la derivata P’(x) è 0.
P’(x)=0 è la seconda equazione proposta che avrà quindi almeno una
soluzione.
per i valori della radice saranno uguale (poiché entrambi 0). allora per il
teorema, esiste almeno un punto tra le due radici dove la derivata P’(x) è 0.
P’(x)=0 è la seconda equazione proposta che avrà quindi almeno una
soluzione.
6.
Si vuole che l’equazione
![]() abbia tre radici reali. Quale è un possibile valore di b? la
funzione
abbia tre radici reali. Quale è un possibile valore di b? la
funzione
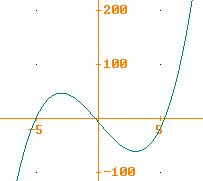 associata y=... è una cubica,
affinchè abbia tre incontri con l’asse x, deve avere un massimo e un minimo;
in più devono essere di segno discorde. Affinchè ci sia un massimo e un minimo
consideriamo la derivata di tale funzione che sarà
associata y=... è una cubica,
affinchè abbia tre incontri con l’asse x, deve avere un massimo e un minimo;
in più devono essere di segno discorde. Affinchè ci sia un massimo e un minimo
consideriamo la derivata di tale funzione che sarà
![]() si annulla per
si annulla per
![]() quindi deve essere b<0 ; tra i vari b possiamo scegliere b= - 27 che da un
massimo e un minimo di segno opposto.
quindi deve essere b<0 ; tra i vari b possiamo scegliere b= - 27 che da un
massimo e un minimo di segno opposto.
![]() esattamente
in 3 e in –3.
esattamente
in 3 e in –3.
soluzione
a cura Toschi Roberto (docente del Liceo ‘Enriques’ di Livorno)
7.Verificare
l’uguaglianza
 e utilizzarla per calcolare un’approssimazione di p, applicando un metodo di
integrazione
e utilizzarla per calcolare un’approssimazione di p, applicando un metodo di
integrazione
numerica.
![]()
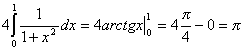 attraverso
un qualsiasi metodo di approssimazione numerica può essere calcolato
l’integrale. provando con 5 intervalli di ampiezza 0,2 e prendendo il punto
medio all’interno dell’intervallo (0.1, 0.3...) otteniamo i valori sotto
elencati, moltiplicando per la base del rettangolo 0,2, sommando le aree così
ottenute e moltiplicando per 4
otteniamo come valore 3,14.
attraverso
un qualsiasi metodo di approssimazione numerica può essere calcolato
l’integrale. provando con 5 intervalli di ampiezza 0,2 e prendendo il punto
medio all’interno dell’intervallo (0.1, 0.3...) otteniamo i valori sotto
elencati, moltiplicando per la base del rettangolo 0,2, sommando le aree così
ottenute e moltiplicando per 4
otteniamo come valore 3,14.
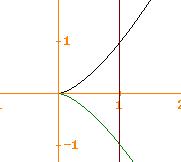 8.
Dare un esempio di solido il cui volume è dato da
8.
Dare un esempio di solido il cui volume è dato da
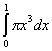 una
possibilità è data dalla rotazione di
una
possibilità è data dalla rotazione di
![]() intorno all’asse x tra 0 e 1.
intorno all’asse x tra 0 e 1.
9.
Di una funzione f(x) si sa che ha derivata seconda uguale a senx e f’(0)=1.Quanto
vale
![]() la
funzione avrà derivata pari a
la
funzione avrà derivata pari a
![]() e questo implica che c = 2 per i
dati
e questo implica che c = 2 per i
dati
quindi
![]() da cui
da cui
![]()
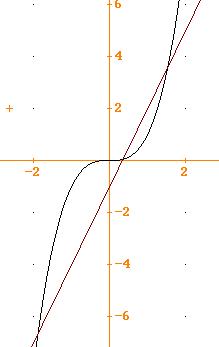 10.
Verificare che l’equazione
10.
Verificare che l’equazione
![]() ammette tre radici reali. Di
una di esse, quella
ammette tre radici reali. Di
una di esse, quella
compresa
tra 0 e 1, se ne calcoli un’approssimazione applicando uno dei metodi numerici
studiati.
per la prima verifica basta
considerate le due funzioni
![]() e
e
![]() e mostrare graficamente che hanno
tre intersezioni che corrispondono alle tre soluzioni dell’equazione data
e mostrare graficamente che hanno
tre intersezioni che corrispondono alle tre soluzioni dell’equazione data
per quando concerne la soluzione da approssimare
considerando che la cubica a ½ vale 1/8 e la retta vale ½
deduciamo che la soluzione
è tale che 0<x<1/2. Stessa osservazione per ¼.
la cubica vale 1/64 mentre la retta vale –1/4. La soluzione
è ¼<x<1/2
Ovvero tra 0,25 e 0,5; provando 0,375 la cubica vale 0.05
mentre la retta 0.125 (la retta sta sopra) 0,25<x<0,375 proviamo per 0,31
la cubica è positiva e la retta negativa (sta sotto) quindi 0,31<x<0,38
ecc.
soluzione
a cura di TOSCHI ROBERTO (docente liceo ‘Enriques’ LIVORNO