28 ottobre ’02

compito di matematica

CLASSE 5 D

Hai domande o reazioni…? scrivi

1) Inscrivi in un triangolo qualsiasi un rettangolo di area massima avente un lato appoggiato sulla base del triangolo, determina inoltre il rapporto tra l’area del rettangolo e l’area del triangolo. (è consigliabile determinare l’altezza del rettangolo chiamando l’altezza del triangolo h e considerandola come nota)

Disegnando un qualsiasi triangolo e indicando con h l’altezza, disegnando all’interno un rettangolo ed in quest’ultimo ponendo l’altezza x avremo che la base del rettangolo (quella che poggia sul lato del triangolo) e anche base di un triangolo simile al triangolo di partenza: sapendo che le altezze sono proporzionali ai lati omologhi scriveremo che dove B è la base del triangolo e b la base del rettangolo, da cui si ottiene . L’area del rettangolo è con 0<x<h. Essendo la funzione in un piano cartesiano una parabola passante per O e per (h,0), rivolta verso il basso , il vertice che avremo per x = h/2 è il valore di massimo che corrisponde da un’area ed essendo l’area del triangolo il rapporto è ½.

2) Sono date due parabole a e b di equazione rispettivamente e con b > a, sia B il punto di b di ascissa 1 (uno). Condotte da B le parallele all’asse x e all’asse y, siano C e A le rispettive intersezioni con la parabola a. Determina (nel risolvere il problema osserva se i dati portato a soluzioni univoche e se il problema è risolubile per qualsiasi valore di a e b)

Il punto B ha coordinate (1,b) il punto A (1,a) . Per il punto C la prima riflessione è chiedersi dove si trova: evidentemente può trovarsi (il testo non lo precisa) nella posizione C’, il problema in questo caso avrebbe poco senso perché quando a tende a b il segmento BC’ sarebbe diverso da 0 e quindi il limite sarebbe facilmente 0.

Quindi consideriamo C nella posizione indicata in figura:

allora avremo che : e quindi il limite è

ovviamente il problema può essere proposto, nello stesso modo con a e b entrambi negativi.

Cosa cambia? Cambiano le rispettive posizioni di B e di C quindi il limite da studiare diventa

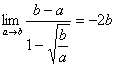e il risultato concorda con il fatto che essendo b negativo –2b è positivo come deve essere il rapporto tra due segmenti.

Non è invece ipotizzabile b>0 e a<0 perché non esisterebbe il punto C.

3) Determina e analizza i punti di discontinuità della funzione:

inoltre disegna il grafico della funzione, mettendo in evidenza gli eventuali asintoti orizzontali o verticali, con motivazione)

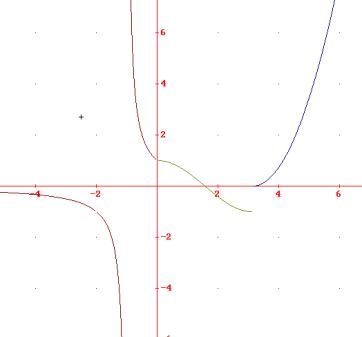
i punti di discontinuità “sicuri” sono x = -2 e x = -1 perché annullano il denominatore della funzione nella zona x<0 quelli da “verificare” sono i punti di raccordo tra le varie rappresentazioni quindi x = 0 e x = p

analizzaziamo tutti i punti

x = -2 la funzione non è definita ma discontinuità di III specie (eliminabile)

x = -1 il limite tende a infinito, discontinuità di II, x = -1 è asintoto verticale

x = 0 non è un punto di discontinuità il limite destro vale 1, quello sinistro vale 1 e la funzione in 0 vale 1.

x = p è di discontinuità di I specie (di salto) il limite sinistro vale –1 il destro 0 e la funzione in p vale 0.

Inoltre _y = 0 è asintoto orizzontale sinistro perché per x che tende a – infinito la funzione tende a 0.

4) Nella funzione (che non occorre disegnarla per intero) individua un asse di simmetria e dimostralo con il metodo che ritieni più conveniente (attento! dimostrare, o meglio in questo caso verificare, non significa far vedere che la simmetria vale per ogni punto della funzione, non solo per qualche punto, anche se può servire per individuare l’asse)

Prima osservazione:essendo una funzione parlando di assi di simmetria possiamo pensare solo ad assi parallele all’asse y.

Dato che questa funzione passa per (0,0) e per (2,0) il possibile candidato è x=1

Modi di dimostrarlo:

se prendo un punto simmetrico all’asse proposto (2-x’,y’) deve verificare l’equazione

come volevasi dimostrare

oppure possiamo spostare l’asse di simmetria con una traslazione x’=x-1 che porti l’asse nell’asse delle y e verificare che la funzione è pari (f(-x)=f(x)) quindi sostituiamo x=x’+1

che una funzione pari per avere la x che compare sempre con esponente pari.

5) Risolvi i seguenti limiti :

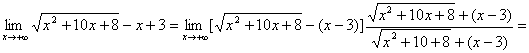
il compito è finito, hai domande o reazioni? scrivi