IL PENDOLO E LE SUE LEGGI

       E' noto a tutti che cosa è un pendolo e come è composto: un filo vincolato ad una estremità alla cui altra estremità è fissata una pallina dal peso P.

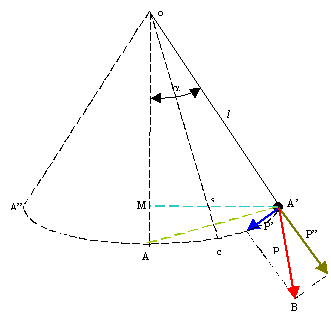
Fig. 1

   La pallina in A' viene lasciata andare. Essa si muove partendo a velocità nulla da A' ad A e poi, con velocità sempre più decrescente, da A ad A", dove la sua velocità diventa nulla. Qui il suo moto si inverte da A" ad A'. Ecco che a questo punto il nostro pendolo ha compiuto una oscillazione completa.

   Da che cosa è causato il moto del pendolo? Semplice: dal peso (della pallina) e dalla forza centripeta.

   Osserviamo la Fig. 1 ed esaminiamo le due componenti del peso P, più precisamente la P" (forza centrifuga) e la P' (direzione del moto della pallina).

   La prima cosa che salta all'occhio è che la P" (forza centrifuga) è equilibrata dalla tensione esercitata dal filo (forza centripeta) e l'unica forza efficace è proprio la P' (direzione del moto della pallina) che costringe la pallina a muoversi con moto vario (P' varia ad ogni istante con il variare della sua distanza s dalla posizione centrale dell'oscillazione).

   Bisogna fare subito una considerazione; se consideriamo un angolo di piccola ampiezza (a<2') avremo che lo spostamento s può confondersi con il rispettivo arco così da poter ritenere in prima approssimazione il moto come rettilineo. In questo caso la forza centrifuga diventa nulla.

   Esaminiamo ora i due triangoli (rettangoli) simili nella Fig. 1 OMA' e BCA' (angolo MOA' e A'BC uguale).

   Se P' è la direzione contraria di s, e avremo:

(1)

e quindi sostituendo

(2)

da cui uscirà che:

(3)

Essendo    costante per un certo periodo del pendolo e per un dato luogo, possiamo affermare che l'accelerazione a del moto è proporzionale ad s; questo corrisponde per quanto già visto in cinematica nel moto oscillatorio dove

(4)

che risolvendola rispetto a T con avremo:

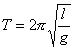(5)

   Questa ultima formula completa le leggi fondamentali del pendolo semplice:

1) la durata dell'oscillazione (perido) è direttamente proporzionale alla radice quadrata dell'accelerazione di gravità ed inversamente proporzionale alla radice quadrata della lunghezza del pendolo;
2) la durata dell'oscillazione è indipendente dalla massa m e dalla natura del pendolo;
3) la durata delle oscillazioni è indipendente dalla loro ampiezza.

    Con il pendolo è possibile dimostrare (come già fatto da Foucault) la rotazione della terra visto che questo strumento oscilla sempre nel medesimo piano; quindi facendo oscillare il pendolo su un supporto fisso noteremo che nelle 24 ore questo avrà disegnato sul basamento una specie di "rosa dei venti"