COMPITO D'ESAME 2007
(pubblicato il 18 giugno 2007)
I
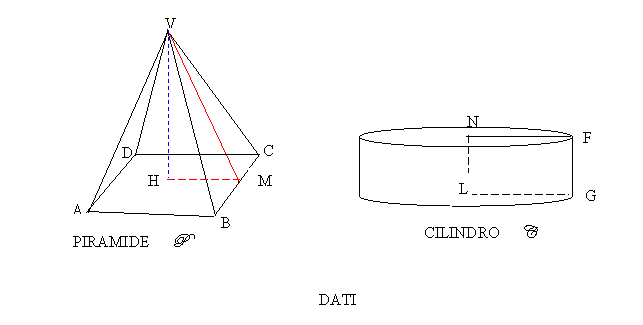
Una piramide regolare quadrangolare ha lo spigolo di base di 14 cm e l'apotema di 25 cm. Calcola l'area della superficie totale di un cilindro equivalente il cui raggio di base misura 10 cm.
FIGURA

P = C ( hanno cioè lo stesso volume)
AB = 14 cm; VM = 25 cm; LG = 10 cm.
PROCEDIMENTO
Mi occorre il volume della piramide e quindi preliminarmente la misura dell'altezza VH:
Da MH = ½ AB = 7 cm, applicando il t. di Pitagora al triangolo rettangolo VHM,
ricavo VH = 24 cm. Pertanto V (Piramide) = 1/3 ABxABxVH = 196 x 24 : 3 = 1568 cm cubi.
Passo al cilindro :
V(cilindro) = 1568 cm cubi
Area di base: A b = p x r x r = p x 100 = 100 p cm quadrati = 314 cm quadrati
Per il calcolo della superficie laterale mi occorre l'altezza NL, che ricavo dalla formula inversa del volume: NL = 3 V / p x r xr = 1568 x 3 : 314 = 14,98 cm.
Superficie laterale:S l = 2 p x r x h = 6,28 x 10 x 14,98 = 940,744 cm quadrati
Superficie totale: S t = S l + 2 x A b = 940,744 + 628 = 499,6 p cm quadrati (circa )
II
Risolvi e verifica:
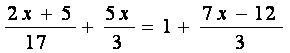
PROCEDIMENTO
Applicando il secondo principio di equivalenza delle equazioni (moltiplico entrambi i membri per il m.c.m. dei denominatori che è 51) ottengo la seguente equazione equivalente all'equazione data:
6x + 15 + 85x = 51 + 119x – 204;
applicando il primo principio di equivalenza delle equazioni, trasporto tutti i termini con l'incognita del secondo membro al primo cambiandoli di segno, e i termini noti del primo al secondo cambiandoli di segno: ottengo così la seguente equazione equivalente alla precedente:
6x + 85x - 119x = 51 - 204 - 15;
da cui, riducendo i termini simili, ottengo:
- 28x = - 168.
Dividendo entrambi i membri per -28 (secondo principio di equivalenza delle equazioni) ottengo la soluzione:
x = 6
VERIFICA:
Sostituendo 6 all'incognita x nell'equazione di partenza avremo:
17/17 + 30/3 = 1 + 30/3
11 = 11.
III
Considera alcuni solidi di vetro (peso specifico = 2,5 g/cm cubi ). Quale relazione lega il peso al volume? Costruisci una tabella di valori relativi ai pesi e ai volumi, quindi riporta tali grandezze in un diagramma cartesiano.
PROCEDIMENTO
La relazione che lega il peso al volume è la legge del peso volumico:
P = V x p s
Nel caso in esame tale legge diventa:
P = 2,5xV
Costruisco una tabella scegliendo per i volumi i seguenti valori e ne ricavo il relativo diagramma cartesiano:
0 - 2 - 4 - 6 - 8
x =V |
y = P |
0 |
0 |
2 |
5 |
4 |
10 |
6 |
15 |
8 |
20 |
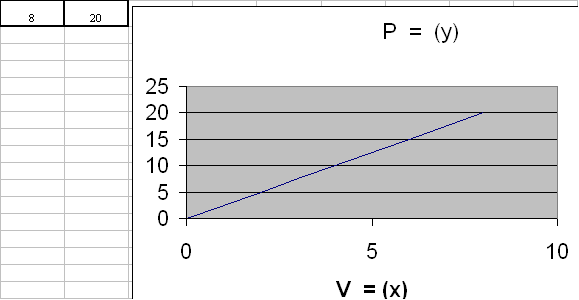
Dal diagramma si rileva che si tratta di una curva lineare (retta) passante per l'origine del riferimento; quindi la legge in esame stabilisce tra le due variabili, dipendente ed indipendente, una proporzionalità diretta: ciò significa che all'aumentare o al diminuire del volume, il peso aumenta o diminuisce in ugual misura.