The easiest examples of motion

The easiest examples of motion are the uniform velocity motion (constant velocity), and the uniform acceleration motion (constant acceleration). In these two cases it’s easy to deduce the analytic laws which rule the motion, and a complete description of motion can be pointed out.

This is a motion during which the instantaneous velocity is always constant.
Hence acceleration is zero.

A constant velocity reveals that:
1)the direction of motion is along a straight line.
2)Average velocity and instantaneous velocity have the same magnitude

By coupling the last relationship with the definition of average velocity, we can build the motion law for all the uniform velocity motions.



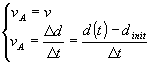
If then , and the last relationship can be written as

As this law shows, the distance versus time graph is a straight line and its angular coefficient is the speed of motion
.

The Uniform Acceleration Motion

This is a motion during which the instantaneous acceleration is always constant.

A constant acceleration reveals that:
1)the direction of motion is along a straight line.
2)Average acceleration and instantaneous acceleration have the same magnitude:

By coupling the last relationship with the definition of average acceleration, we can build the velocity law for a uniform acceleration motion



If then , and the last one can be written as

The velocity versus time graph is a straight line and its angular coefficient is the motion’s acceleration .

From this graph the relationship between the average velocity and the instantaneous velocity can be deduced. It follows from the idea of a segment’s average point:

By coupling this with the previous equation (2) and with the definition of average speed, we have a three equation system. Its solution represents the law of motion for uniform acceleration motion:

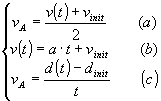
By inserting the (b) into the (a) we have:

and by inserting the (c) into the last one:

that leads to:

The graph of this motion law is a branch of a parabola. For instance, if the initial distance and the initial velocity are equal to zero, the diagram is similar to the following one:

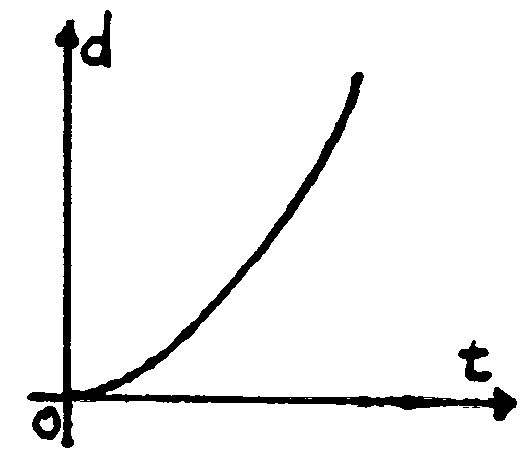
The parabolic behaviour is strictly related to the square dependence on time.

Index...