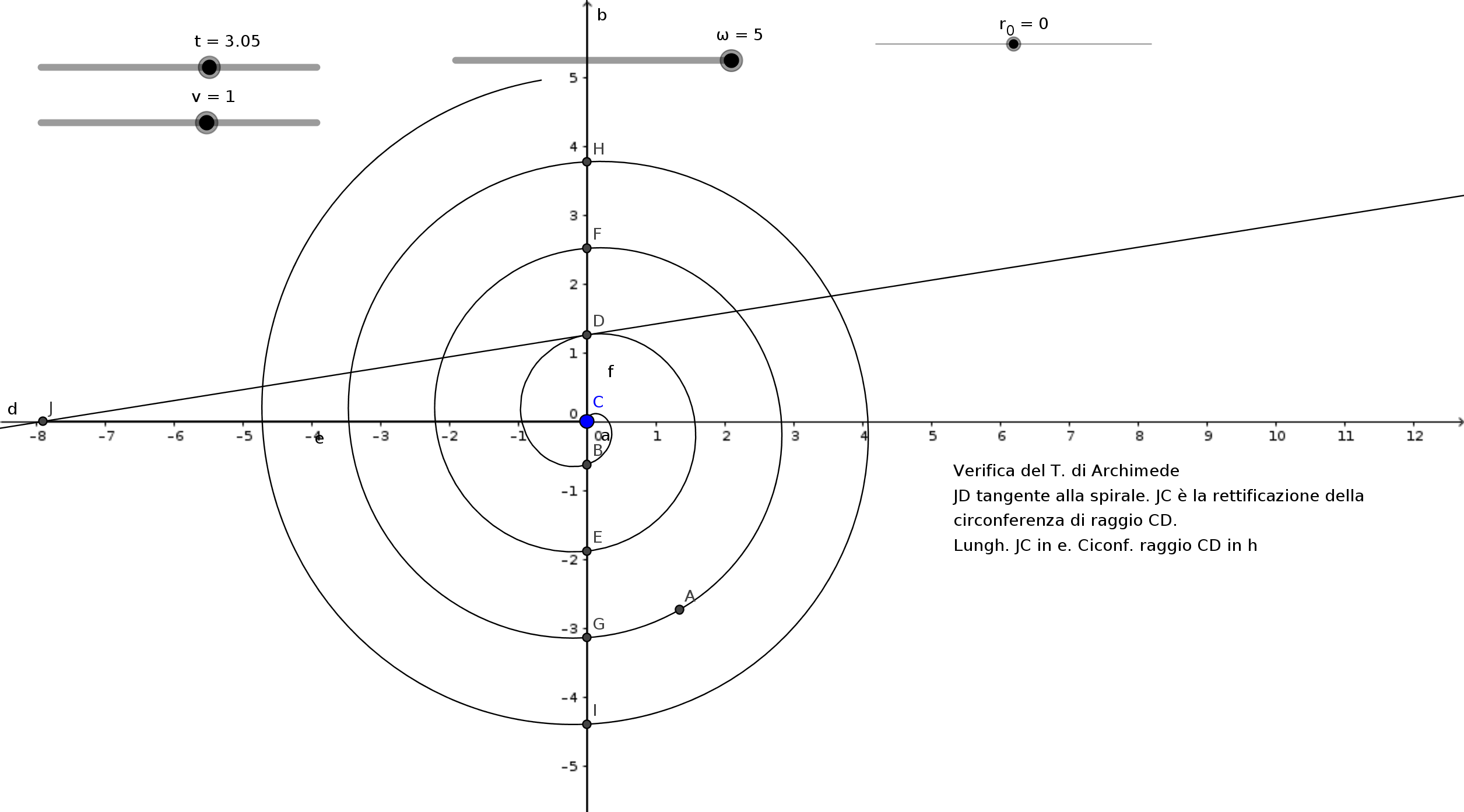
Per disegnare una spirale con GeoGebra si deve intanto definire una variabile tempo t, una velocità v del punto A, una velocità angolare ω della retta su cui viaggia A. Per ciascuna di queste tre variabili si possono definire i cursori (slider) per cambiarne il valore.
Ovviamente la distanza r percorsa da A sulla retta è data da:
r=v . t
Nella riga di comando di GeoGebra si può scrivere questa relazione definendo una nuova variabile r. L'angolo descritto dalla retta è dato da:
α = ω .t

L'ascissa m del punto A si può ottenere nel seguente modo:
m= r . cos(ω .t)
Analogamente l'ordinata n di A:
n= r . sin(ω .t)
Anche queste equazioni vanno scritte nella riga di comando di GeoGebra tenendo conto che la moltiplicazione si indica con *
e la funzione sen con sin.
Si tratta adesso di definire il punto A:
A=(m,n)
Il risultato sarà che al variare di t con lo slider, il punto A descriverà la spirale.
E' possibile attivare la traccia lasciata da A.
La sciando v=0, si otterrà solo rotazione. Ponendo ω=0, si avrà solo traslazione.
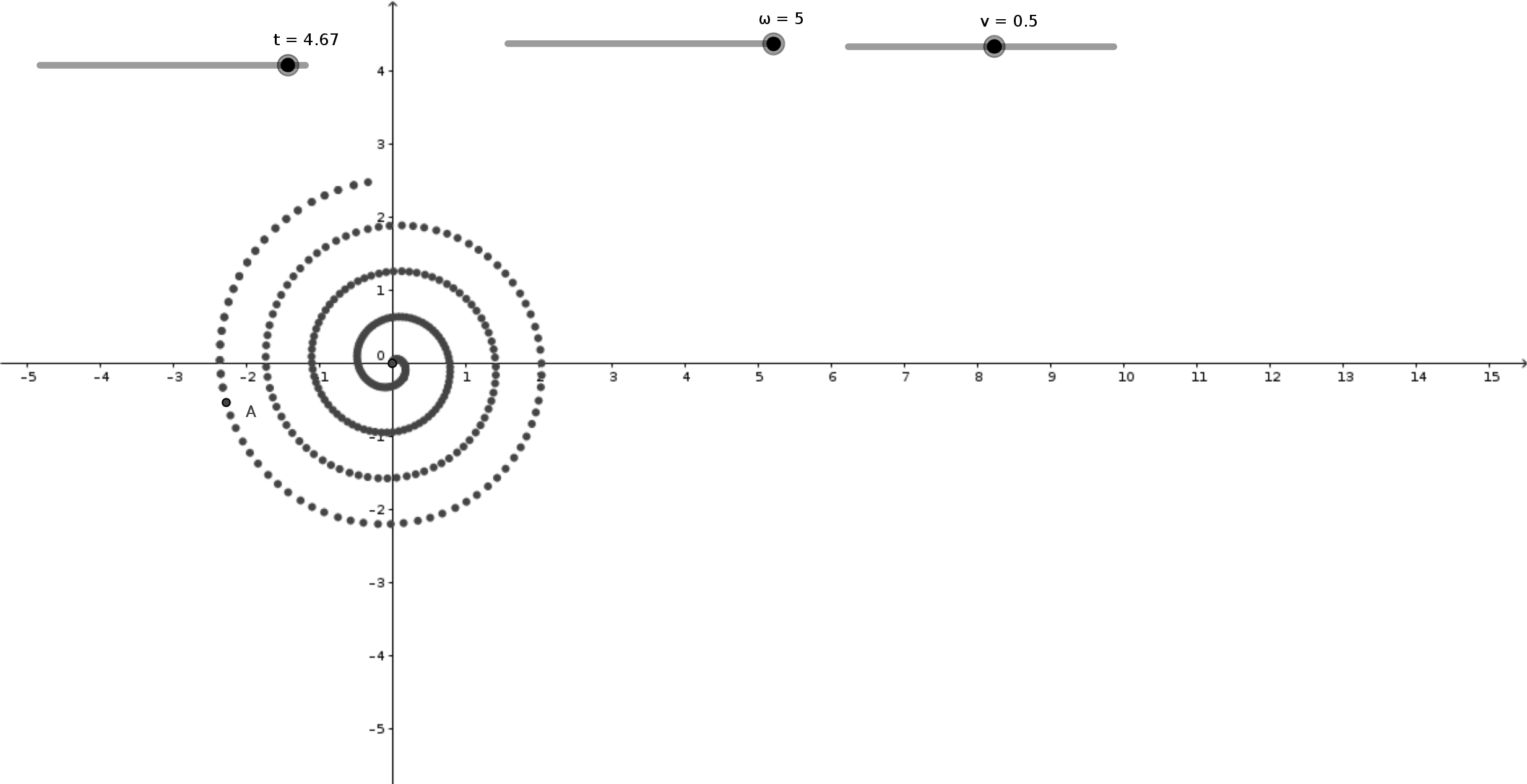
Si può definire in GeoGebra la spirale come curva parametrica:
Curva(v t cos(ω .t), v t sin(ω .t), t, 0,5)
Il parametro è t che varia fra 0 e 5.
In questo modo si possono ottenere i punti di incontro con l'asse y della spirale e le tangenti alla spirale stessa.