LA COSTRUZIONE DELLA

SCALA PITAGORICA

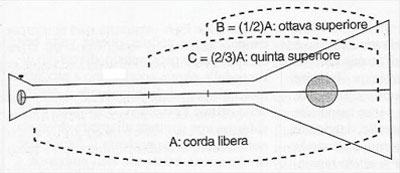
Qui di seguito Fabio Bellissima spiega passo passo come Pitagora sia riuscito nella sua opera.

"Vi è  un settore, poco visibile ma basilare e di rigida pertinenza musicale, nel quale la simmetria in tutte le sue forme ha un ruolo importante: è quello della scelta dei suoni della scala.

In effetti, il problema dell' accordatura è così "di base" che sovente non viene neanche rilevato. Eppure le singole note, che troviamo sulla tastiera di un pianoforte così come su quella di un flauto, costituiscono l'alfabeto con cui costruire una qualunque composizione musicale.
Con quale criterio sono stati scelti proprio quei suoni e, soprattutto, come sono state determinate le distanze tra uno e l' altro? In genere, quando si suddivide un intervallo continuo lo si fa con punti equidistanti, e infatti, come attestano vari strumenti musicali antichi, alcuni tentativi si mossero in questa direzione.

Essa tuttavia fu presto abbandonata, perché il criterio che è alla base della scelta dei suoni non è quello spaziale di equidistanza, bensì quello musicale di consonanza. Questo concetto, nei manuali di teoria, è così definito: un intervallo tra due note si dice consonante se, suonando le due note simultaneamente, si ottiene un effetto di gradevolezza e di quiete; si dice invece dissonante se produce un senso di instabilità e di tensione.

I termini impiegati ("gradevolezza", "tensione", "quiete") possono indurre a pensare che i giudizi sulla consonanza siano vaghi e soggettivi; invece, almeno per quanto riguarda le consonanze fondamentali, hanno valore pressoché universale. In qualunque parte del mondo, quando un uomo e un bambino cantano uno stesso motivo, non emettono suoni uguali in altezza, ma ad altezze distinte che tuttavia formano costantemente tra loro un intervallo che noi chiamiamo di ottava.

La sensazione di consonanza che due suoni posti a tale intervallo producono è tale che la nomenclatura musicale, da Guido d' Arezzo in poi, attribuisce loro lo stesso nome (do-do, re-re eccetera), salvo impiegare indici o apici per distinguerli quando è necessario (do1-do2, re1-re2). I Greci, dal canto loro, pur non nominando le note modulo un'ottava, attribuivano a questo intervallo il nome di diapason (dia-pason, attraverso tutto) per significare che in esso è contenuto l'intero campionario delle note.

Quella di ottava non è l'unica consonanza "universale". Se all'interno di tale intervallo si deve trovare un suono centrale, la scelta, nella pressoché totalità dei casi, cadrà su una nota che forma con la nota bassa dell'ottava un intervallo di quinta e, conseguentemente, un intervallo di quarta con la nota alta.
Secondo la teoria di Helmoltz, due suoni sono avvertiti come consonanti se hanno molti armonici in comune, e i suoni ad intervallo di ottava sono quelli che ne hanno il maggior numero, seguiti da quelli a intervallo di quinta. Ma la spiegazione fisica serve a giustificare una oggettività che è evidente di per se; inoltre tale spiegazione, pur complessa, ha alla base un dato di immediata rilevazione.

Se prendiamo una corda che produce un determinato suono e desideriamo ottenere il suono superiore di un'ottava, dobbiamo interrompere la corda nel suo punto centrale. Indicando con A la lunghezza della corda che produce il primo suono e con B la lunghezza della sezione che produce il secondo, abbiamo che A: B = 2 :1.
Per salire di una quinta, dobbiamo interrompere la corda ai due terzi e quindi, indicando con C la lunghezza della sezione che produce questo nuovo suono, abbiamo A:C = 3:2. Infine, i suoni prodotti dalle corde C e B formano un intervalli di quarta, e C:B = 4:3. Abbiamo quindi che le tre consonanze principali, ottava quinta e quarta, corrispondono ai rapporti 2:1; 3:2 e 4:3 e possono essere rappresentate impiegando, e in modo "regolare", solo i primi quattro numeri naturali. 

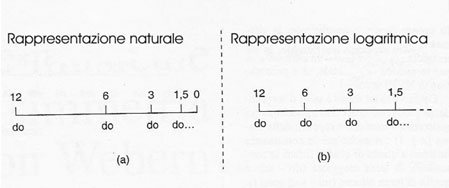
All'interno della loro scuola fu sancita la quadripartizione della matematica in aritmetica-musica-geometria-astronomia (distinzione protrattasi fino al "quadrivium" medioevale), e la determinazione degli intervalli della scala rimase a lungo il più frequentato campo di applicazione della teoria delle proporzioni. Ma non è solo questo il tipo di simmetria a essere coinvolto nel problema dell' accordatura della scala; anche la simmetria nel significato moderno ha avuto in tale processo un ruolo importante, sebbene più problematico.

Innanzitutto, per poter parlare di simmetria in senso spaziale bisogna, ovviamente, dare una rappresentazione spaziale della scala musicale, e qui si incontra subito una difficoltà. Consideriamo due intervalli musicali, siano A e B le lunghezze delle corde che producono i due suoni del primo intervallo e C e D le lunghezze relative al secondo intervallo. Da un punto di vista musicale, i due intervalli sono percepiti come uguali se A/B = C/D e non se A-B = C-D, come il termine "intervallo" potrebbe indurre a credere.

Supponiamo ora che una corda, ad esempio di lunghezza 12, produca un suono che indichiamo con do. I tre do delle ottave successive corrisponderanno a sezioni di corda di lunghezza 6, 3, 1,5. Una rappresentazione "naturale", cioè che rispetti le distanze e quindi descriva la reale posizione dei suoni su una corda, è come nella parte sinistra dello schema questa pagina in alto.
Ma una rappresentazione che rispetti l'intuizione musicale deve essere invece come nella parte destra dello schema. Questa seconda rappresentazione, logaritmica, attribuisce infatti lo stesso spazio a due intervalli quando essi sono uguali in senso musicale, cioè quando i rispettivi estremi stanno nello stesso rapporto.

Chiaramente, la presenza di simmetrie (nel significato moderno) dipende dal tipo di rappresentazione impiegata; e poiché quella logaritmica descrive correttamente la sensazione musicale, è a essa che storicamente ci si è riferiti. Ora, se all'interno dell'ottava compresa tra il do di corda 12 e il do di corda 6 inseriamo due note che producano con il primo do rispettivamente un intervallo di quarta (4:3) e di quinta (3:2), individueremo le sezioni di corda di misura 9 e 8. Infatti 12:9 = 4:3 e 12:8 = 3:2. Chiamiamo fa e sol queste due nuove note.

Se, invece di rappresentarla in modo metrico, rappresentiamo la scala composta da questi quattro suoni in modo logaritmico, essa evidenzia una perfetta simmetria assiale, essendo costituita da due intervalli di quarta (12:9 = 8:6 = 4:3) separati al centro da un intervallo espresso dal rapporto 9:8, che i Greci chiamarono tono (e che esprime la differenza tra una quinta ed una quarta). L'insieme dei quattro numeri 12,9,8, 6 e dei loro reciproci rapporti venne, dai Pitagorici in poi, rappresentato innumerevoli volte, sempre in modo da evidenziare la simmetria; il suo fascino, accresciuto dal fatto che 9 e 8 sono rispettivamente la media aritmetica e la media armonica tra 12 e 6, esercitò a lungo un richiamo molto forte.

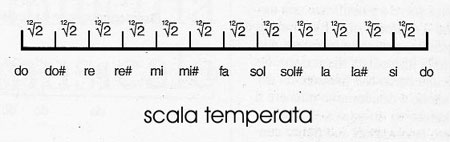
Nicomaco da Gerasa (I secolo d.C) chiamò la quaterna 12-9-8-6 "divina proporzione", per la sintesi perfetta di armonia musicale, rapporti numerici e simmetria spaziale, e fino all'età del temperamento (cioè fino al Settecento) essa rappresentò la base comune a tutte le accordature della scala. Aggiungendo nella parte (b) dello schema una nota all'interno di ciascun intervallo di quarta si hanno complessivamente cinque note diverse, cioè una scala pentatonica, aggiungendone due si ha una scala eptatonica.

Il desiderio di aggiungere tali note in modo da dividere la quarta in due o tre parti uguali tra loro, in modo da ottenere una disposizione simmetrica (nel significato moderno), si è trovato in conflitto con la simmetria nel significato antico: infatti, poiché uguaglianza di intervalli significa uguaglianza di rapporti, la metà di un intervallo di estremi A e E è espressa dal medio proporzionale, cioè dal punto x tale che A:x = x:E.
Analogamente, dividere un intervallo in N parti uguali significa trovare N medi proporzionali. Ora, un teorema dovuto al pitagorico Archita e riportato nella Sectio Canonis di Euclide asserisce: se A:E = (N+1):N, allora tra A e E non esistono ne uno ne più medi proporzionali (che siano numeri naturali).

Poiché tutte le consonanze finora incontrate -ottava, quinta, quarta - sono espresse da rapporti della forma (N+1):N, il teorema di Archita sancisce l'incompatibilità tra la simmetria nel significato antico e l'equipartizione razionale di intervalli consonanti. In questo rapporto conflittuale, la simmetria nel significato antico ha prevalso incondizionatamente per un periodo che, per la musica occidentale, si è protratto fino al XVIII secolo.

Decisivo in tal senso è stato il sorprendente perdurare della corrispondenza tra consonanze musicali e rapporti della forma (N+1):N anche per le consonanze inferiori a quella di quarta. Infatti la consonanza di terza maggiore (do -mi) e quella di terza minore (mi-sol) sono rispettivamente espresse dai rapporti 5:4 e 6:5. Le note all'interno dell'intervallo di quarta sono state aggiunte in modo da ottenere una di queste due nuove consonanze.

Aggiungendo, in ciascuna quarta, una nota che produca un intervallo di terza maggiore con la nota grave della quarta stessa, avremo la più antica scala enarmonica greca (pentatonica), mentre aggiungendo per ciascuna quarta una nota che formi un intervallo di terza maggiore con la nota acuta della quarta stessa avremo la scala pentatonica che è tuttora la scala nazionale del Giappone. Impiegando invece l'intervallo di terza minore otteniamo, aggiungendo una nota che formi tale intervallo con la nota bassa della quarta, la più antica scala cromatica greca, ancora in uso in oriente (Cina e Mongolia) e in Scozia (la popolarissima Auld lang syne può essere suonata con le note di questa scala). Anche se le scale pentatoniche sono, sufficientemente espressive, la cultura musicale occidentale è approdata, già in antico, a una scala eptatonica, ottenuta aggiungendo sempre nella parte b dello schema  in basso due note all'interno di ciascuna quarta.

Tra le tante scale eptatoniche proposte (Tolomeo, nei suoi Elementi Armonici, ne elenca oltre quindici), quella che contiene il maggior numero di consonanze e che si è imposta in tutto l'occidente è la "scala giusta", detta anche "scala naturale" o "scala dei fisici". È questa la scala che, se non si è stonati, si percorre cantando do-re-mi- fa-sol-la-si-do. La simmetria assiale di cui godevano le note non si è estesa alle nuove; per contro, si è conservata una forte simmetria nel significato antico: ogni intervallo tra una nota e la successiva è espresso da un rapporto (N+1):N.
Questa scala, salvo lo scambio delle ampiezze tra gli intervalli sol-la e la-si, fu proposta per la prima volta da Didimo, un teorico greco vissuto tra il I e il II secolo d. C. È significativo questo fatto: i greci, per motivi non ben chiari ma presumibilmente di natura non solo estetica, ritenevano non consonanti gli intervalli di terza maggiore e terza minore.

Didimo quindi pervenne alla scala giusta solo in base a considerazioni di regolarità numerica. Eppure alla fine del secolo XVII, la simmetria nel significato moderno si  prende, sempre sul campo dell'accordatura della scala, una notevole rivincita sulla simmetria nel significato antico. I nomi do, re mi eccetera che abbiamo fin qui impiegato devono essere intesi in senso relativo, come primo, secondo, terzo grado della scala; infatti, ciò che è determinato nelle scale non è l'altezza assoluta delle note, ma il rapporto tra le altezze. poiché cantanti diversi vorranno impiegare altezze diverse nell' esecuzione di uno stesso brano, è importante, se l'accompagnamento deve esser eseguito da uno strumento a tastiera, che tale strumento sia in grado di produrre diverse gamme di suoni.
Inoltre, queste diverse gamme possono essere impiegate all'intemo di uno stesso pezzo; un tale passaggio, che costituisce un cambio di tonalità, aumenta le capacità espressive della musica.

Ora, un cambio di tonalità è una variazione proporzionale dell'altezza di tutte le note e quindi corrisponde a una traslazione orizzontale. Consideriamo una tastiera ottenuta congiungendo delle ottave tutte accordate allo stesso modo: diciamo che questa tastiera ammette una traslazione di ampiezza T se, dopo uno spostamento verso destra di tale ampiezza, ogni nota si trova a occupare una posizione già occupata da una nota prima della traslazione.
Se le ottave della nostra tastiera sono accordate conformemente alla scala giusta, allora la minima traslazione possibile è quella avente per ampiezza un' ottava. Ciò significa che su una simile tastiera non si possono effettuare cambi di tonalità. Una strada a lungo tentata per superare in parte questa situazione è stata quella di lasciare inalterati i suoni della scala giusta e aggiungere altri suoni fra di essi, in modo da poter produrre più di una tonalità.

Ma, alla fine del Seicento, si è imposta una soluzione più drastica. Il massimo numero possibile di traslazioni si ottiene se l' ottava è divisa in parti uguali. Essendo l' ottava espressa dal rapporto 2:1, che ha la forma (N+1):N, il Teorema di Archita sancisce l'impossibilità di ottenere una qualunque equipartizione mediante rapporti tra numeri naturali; ed essendo tutte le consonanze espresse da rapporti di questo tipo, una qualunque divisione dell'ottava in parti uguali non potrà contenere al suo interno alcuna consonanza giusta.
Tuttavia, l' orecchio sopporta bene piccoli errori rispetto all'intonazione esatta; confidando su questo fatto, si è scelto di dividere l' ottava in un numero N di parti uguali, scegliendo N in modo tale da poter approssimare soddisfacentemente le note della scala giusta.

Ora, l' ottava ha una ampiezza di circa sei toni (come riporta Euclide nella Sectio Canonis, sei toni determinano un rapporto 531441/262144, di poco superiore a due); ma, avendo l'intervallo di quarta un' ampiezza di circa due toni e mezzo e quello di quinta di circa tre toni e mezzo, per approssimare tali intervalli è necessario disporre di mezzi toni: il numero sei deve essere moltiplicato per due.
Nasce il tal modo la scala temperata, quella dei moderni pianoforti, in cui l'ottava è divisa in dodici intervalli uguali.

L 'accettazione del temperamento non rappresenta tuttavia il trionfo della seconda sulla prima, bensì il raggiungimento di un compromesso. Del resto, il fatto che la tastiera del pianoforte abbia la sua attuale disposizione testimonia che la scala temperata è un ambiente matematicamente simmetrico disposto, fisicamente, in modo asimmetrico, al fine di potere ben approssimare, con la scala dei tasti bianchi e le sue traslazioni, l' antica simmetria delle proporzioni e delle consonanze."