MUSICA, UNA PASSIONE MATEMATICA

Sommario.
«Musica est exercitium arithmeticae occultum nescientis se numerare animi», ossia "Musica è un esercizio aritmetico della mente che conta senza sapere di contare": così scrisse Leibniz, forse ispirandosi all'idea pitagorica che il segreto dell'armonia risieda nel magico potere dei numeri.
Da quel tempo lontano la musica ha fatto enormi passi, al punto che i canoni di consonanza/dissonanza alla base dell'armonia classica appaiono oggi superati e anzi decisamente limitativi dell'innovazione musicale.
Eppure le più recenti scoperte della psicoacustica sembrano suggerire che quella di Leibniz fu un'intuizione profonda, che in qualche modo corrisponde a criteri di fondo per la comprensione e l'apprezzamento del suono musicale.
Si parlerà dei meccanismi che permettono al sistema orecchio-cervello di definire, per un suono anche molto complesso, una precisa altezza, talvolta virtuale, di amalgamarlo in un timbro unitario e compatto, e in sostanza di avere delle preferenze naturali per insiemi di suoni che rispettino determinate condizioni di periodicità temporale, legate a una strutturazione armonica o tale da potersi ad essa assimilare.

I. INTRODUZIONE

Prendo l'avvio da una frase molto significativa di Pierre Boulez: «La musica non può progredire senza la scienza». Pronunciata mezzo secolo fa, essa appare oggi quasi ovvia. La argomenta bene John Pierce, il pioniere dell'elettronica musicale: «I geni del passato possono essere un peso per il presente. Quanta musica contemporanea resiste al confronto? Forse possiamo evitare di rimanere schiacciati solo con nuove tecniche e nuove conoscenze che essi non possedevano». Alcuni compositori degli ultimi decenni hanno accolto questi argomenti con tanto zelo, da utilizzare spesso l'innovazione formale come fine a se stessa, quasi fosse un surrogato del talento.

Possiamo ricordare sotto quali profili il ruolo della scienza si esplica più incisivamente. Prima di tutto, nel mettere a disposizione le straordinarie potenzialità dell'elettronica e dell'informatica: al di là degli eccezionali progressi nella riproduzione del suono, al compositore si aprono nuove prospettive in fatto di sonorità, di timbri, di mezzi espressivi. In secondo luogo, nel permettere una migliore progettazione degli stessi strumenti acustici tradizionali e una valutazione oggettiva dei loro meriti, oggi quantificabili. Terzo ambito, il più suggestivo, quello della psicoacustica, dove l'obiettivo ultimo potrebbe essere quello di individuare le risorse e le limitazioni del "consumatore" di suono musicale, in vista di una innovazione che non risulti sterile (chi non si chiede, tra i frequentatori delle sale da concerto, perché tanta produzione del Novecento, a cent'anni di distanza dalla rivoluzione schoenberghiana, viene ancora rifiutata dal vasto pubblico e suscita soltanto l'interesse professionale degli addetti ai lavori?).

Alcuni quesiti della psicoacustica musicale sono ad esempio: esistono aspetti biologici nei criteri di consonanza/dissonanza tramandatici attraverso i millenni dai cinesi prima e dai greci poi? C'è forse una base ontogenetica nella nostra quasi istintiva preferenza della cosiddetta armonia tonale classica e nel rifiuto di talune forme di negazione della stessa? Per esempio, qual è l'origine del nostro "senso" per certi intervalli musicali? E in questo, che ruolo gioca la relazione con l'ambiente naturale - suoni come voci, corde e canne - e quanto invece l'esposizione a quello culturale? Fino a che punto questo può sovvertire il primo? Un classico tema della psicoacustica che può aprire finestre su tali questioni è come il sistema uditivo, di fronte a suono complesso, persino quando è fatto di componenti che non stanno fra loro in rapporti armonici, giunga ad assegnargli un pitch, ossia una precisa altezza che permette di collocarlo sul pentagramma.
È questo un punto chiave, giacché informa sui modi in cui il processore centrale del sistema nervoso elabora ed organizza i segnali provenienti dagli organi periferici. E come può (o non può) pervenire al loro apprezzamento.

In assenza di adeguati mezzi di indagine, nella seconda metà del Novecento, dopo una lunga resistenza alla rottura dei canoni tradizionali dell'armonia, nell'ambito dei critici e dei musicologi sembra essere stata accettata in pieno - ossia fino agli estremi limiti - l'idea di Schoenberg della dominanza dell'assuefazione culturale sui presupposti biologici. E appare accolta anche da una certa parte dei compositori e da una minoranza del pubblico. Oggi dovrebbero esistere, tuttavia, sufficienti capacità di comprensione e adeguato potenziale tecnologico per riprendere in mano la problematica e stabilire se nella musica vi siano, e quali siano, eventuali esigenze inderogabili del corpo e della mente. A tutto vantaggio della musica futura.

Che la musica fosse imparentata con le scienze era già un fatto acquisito nel Medioevo, allorché essa veniva annoverata tra le arti del quadrivio insieme ad aritmetica, geometria e astronomia. Imperava allora la celebre frase di Pitagora: «Il segreto dell'armonia risiede del magico potere dei numeri», concetto nato dalla constatazione che gli intervalli consonanti di ottava, quarta e quinta perfetta corrispondono a note le cui frequenze stanno fra loro in rapporti di numeri piccoli interi (do-do', 1:2; do-sol, 2:3; do-fa, 3:4, con 1+2+3+4=10, il numero magico).

Nel Settecento, con Leibniz, si torna parlare di numeri, ma nelle sue parole la cabala è del tutto svanita
«Musica est exercitium arithmeticae occultum nescientis se numerare animi»
ossia:
«Musica è un esercizio aritmetico della mente che conta senza sapere di contare».
Attenzione a questo concetto, così straordinariamente presago di allora insospettate verità! Mostrerò, in quanto segue, che l'affermazione di Leibniz si può con ragione applicare alle odierne conoscenze scientifiche, vale a dire alle correnti interpretazioni di come lo stimolo sonoro periferico generi impulsi elettrici diretti al cervello e di come quest'ultimo operi per organizzarli.

Naturalmente mi riferirò a un cervello naïf, un cervello che non abbia percorso la via dell'affinamento musicale e non abbia ancora appreso a interpretare stimoli di elevata complessità, arrivando a trarre dalla complessità stessa motivi di più profondo apprezzamento. Un cervello che risulti quindi meglio soddisfatto allorché può operare in maniera naturale, come chi abbia la possibilità di esprimersi nel gergo nativo anziché in una lingua straniera.[4]

Un cervello com'era, in un certo senso, quello degli uomini acculturati del Settecento, un cervello incapace di immaginare la successiva evoluzione dell'arte musicale: dall'armonia classica - basata sulla tonalità e sulla consonanza degli accordi - all'armonia tonale arricchita da dissonanze o realizzata in ambiente del tutto dissonante, sino a forme varie di pluritonalità, microtonalità, o atonalità. In altre parole, dai primi passi nell'emancipazione dai concetti di centro tonale e di dissonanza, fino alla totale dissoluzione di qualsiasi residuo dell'armonia cinese e poi greca, senza riguardi per quella sua eventuale maggiore oggettività fisio-psicologica, rispetto a scelte alternative, che certi risultati della ricerca psicoacustica sembrano oggi suggerire.

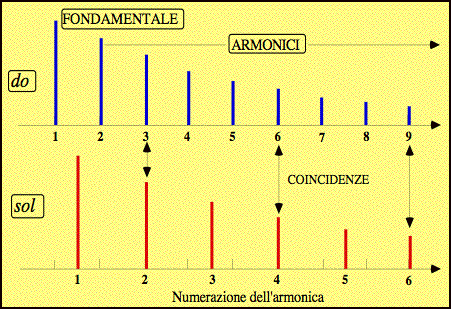
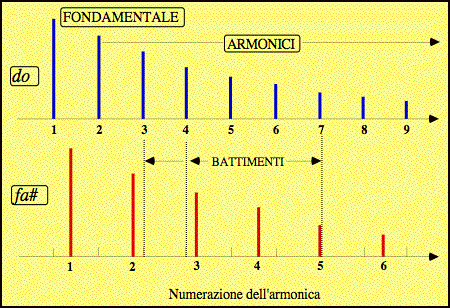
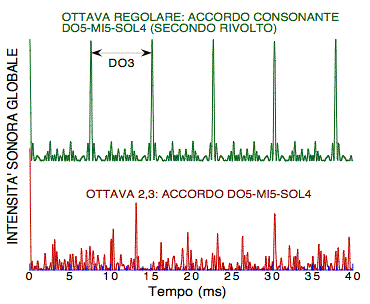
II. L'IPOTESI DI HELMHOLTZ

Il primo approccio scientifico alla ricerca di un'origine oggettiva della dualità consonanza/dissonanza classica è dovuto a Hermann von Helmholtz, il grande studioso ottocentesco dei problemi della percezione acustica e visiva.[5] Egli ritenne di poter ascrivere la dissonanza all'eventuale presenza di battimenti tra gli armonici dei suoni complessi costituenti l'accordo musicale (allorché due suoni hanno frequenze molto vicine, si produce una modulazione dell'ampiezza - una sorta ululato - non gradevole all'ascolto, anche se utile nell'accordatura degli strumenti).
È utile ricordare che i suoni reali - quali sono le note emesse dagli strumenti musicali - sono costituiti da un tono fondamentale più le sue armoniche o armonici o ipertoni, ossia componenti di frequenza multipla del primo (si veda in Fig. 1 il confronto tra un tale suono e il la fondamentale emesso da un diapason, che è invece un suono puro).

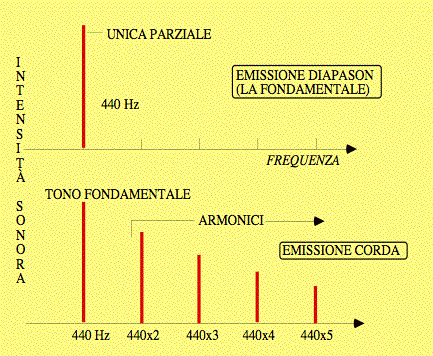
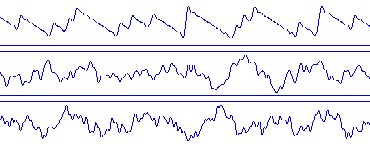
Fig. 1. Sopra: l'energia acustica di un suono puro, com'è quello di un diapason, è concentrata a una sola frequenza (tono fondamentale). Sotto: nel suono emesso da una corda, l'energia acustica è invece distribuita su diverse componenti, o parziali, di frequenza multipla della fondamentale e di intensità via via decrescente.

 Benché la suggestiva idea di Helmholtz sia da non pochi accettata per buona ancora al tempo presente, negli anni tra il 1960 e 1970, un intelligente esperimento fatto all'IRCAM di Parigi da John Pierce, scienziato, e Pierre Boulez, musicista,[6] ne ha dimostrato la sostanziale erroneità: non solo la condizione di assenza di battimenti per avere consonanza non è sufficiente, ma forse nemmeno necessaria.

III. L'OTTAVA ESPANSA

Nell'esperimento di Pierce e Boulez, anziché prendere il fattore di ottava[7] naturale, ossia 2, se ne adotta uno maggiore. Ciò significa escludere che tra le note della scala, così come tra le parziali all'interno di ciascuna nota, sussistano rapporti armonici. Suoni in ottava espansa si possono realizzare soltanto con strumenti sintetici, o con il computer, in quanto i normali strumenti basati su corde o canne hanno in via naturale una strutturazione armonica (si riveda la Fig. 1).
Nello schema sottostante è mostrato come viene ad alterarsi la serie delle frequenze formanti una nota musicale nel passare da un fattore di ottava 2 a uno 2,4 (si è preso il valore 1 per la frequenza del tono fondamentale):

         1           2           3           4            5          6            7            8           9          10         11…

         |            |            |            |             |            |            |            |             |            |           |

         |                  |                   |                       |                       |                         |

        1              2,40                4                  5,76                  7,60                   9,60

Nel caso di un accordo di due o più note, le eventuali sovrapposizioni di parziali si conservano, ma poiché si ampliano tutti gli intervalli, aumenta la separazione tra le parziali e si riduce così la possibilità di battimenti. I caratteri di dissonanza e consonanza, nella visione di Helmholtz dovrebbero mutare: gli accordi dissonanti potrebbero divenire consonanti, gli accordi consonanti non dovrebbero peggiorare. Insomma, un insieme di note non dovrebbe risultare mai meno consonante di come si presenta con fattore di ottava 2.

È particolarmente istruttivo esaminare la forma d'onda di una singola nota in ottava espansa e in ottava regolare, così come quella di un accordo triadico, ad esempio di tonica do-mi-sol. Le onde sono state generate al computer prendendo per ogni nota 9 armoniche di ampiezza decrescente in ragione inversa del loro numero d'ordine (tipico suono di corda) e tutte in fase tra loro (questa scelta è resa possibile dal fatto che, nella percezione di un suono complesso, l'eventuale sfasamento tra le varie parziali non ha praticamente alcun effetto, lasciando altezza e timbro immutati). Ciò è mostrato rispettivamente nelle Figure 4 e 5.

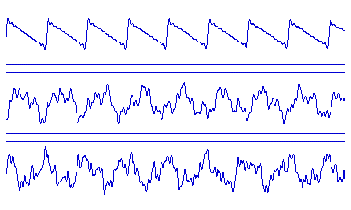
Fig. 4. In alto: l'andamento temporale dell'onda di una nota di corda in ottava regolare ha una caratteristica forma a dente di sega e una perfetta periodicità. Al centro e il basso: espandendo l'ottava, la forma d'onda diventa sempre più irregolare e la periodicità si dissolve, ossia in ogni periodo l'onda muta aspetto.

Fig. 5. In alto: l'andamento temporale della forma d'onda di un accordo in ottava regolare, pur nella sua relativa complessità, presenta una perfetta periodicità. Al centro e in basso: in ottava espansa la forma d'onda diventa irregolare e la periodicità si dissolve.

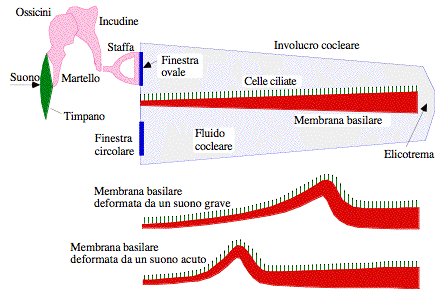
In conclusione: il meccanismo suggerito da Helmholtz è del tutto inoperante. La gradevolezza dei suoni musicali appare piuttosto legata alla possibilità del sistema percettivo di poter assegnare al suono tre attributi principali:

     - un carattere di unitarietà e di fusione delle varie frequenze che lo compongono

     - un timbro ben definito e compatto

Tali condizioni si realizzano allorché l'insieme delle parziali presenta:

     - una strutturazione armonica, come avviene nei suoni naturali, ossia quelli emessi da corde e canne, nonché quelli vocali, tale requisito dovendosi estendere anche alle relazioni tra più note suonate assieme

     - una ben definita periodicità dell'onda (per gli esperti, i due requisiti sono soddisfatti se l'onda sonora è espandibile in serie di Fourier).

Se la strutturazione non è armonica, il sistema percettivo non è particolarmente disturbato fintanto che gli riesce di assegnare al suono un timbro e un'altezza, in certo senso equiparandolo a una serie armonica approssimata.[11]
È questo il caso degli strumenti inarmonici - campane tubolari, timpani, e certi suoni generati sinteticamente - che permettono di intonare melodie e si mostrano compatibili con gli strumenti armonici dell'orchestra, ossia archi e fiati.

 Nel caso dei suoni puri - non formati da più frequenze - il meccanismo di assegnazione del pitch da parte del cervello è di carattere posizionale. La membrana basilare, ossia il filamento interno alla coclea che entra in oscillazione quando, attraverso la catena degli ossicini, riceve la perturbazione timpanica, si veda la Fig. 6, si deforma in modo diverso a seconda della frequenza dell'onda acustica ricevuta: più alta è la frequenza in arrivo, più il massimo di deformazione della membrana basilare si trova sul lato degli ossicini.
Lungo la membrana basilare corrono delle terminazioni nervose, le celle ciliate: la loro configurazione di eccitazione risulta quindi caratteristica per ciascuna frequenza, ed è questo il tipo di informazione che il cervello utilizza per individuare l'altezza della nota.
Quanto all'intensità del suono,  le terminazioni nervose attivate inviano al cervello un treno di impulsi che è tanto più fitto nel tempo quanto più il suono è forte (questo è il primo e più ovvio aspetto della funzione di conteggio svolta dal cervello).

 Nel caso dei suoni reali, costituiti da molte frequenze, le cose non sono così semplici, perché sulla membrana basilare si hanno simultaneamente molteplici siti di elevata eccitazione. Eppure il cervello giunge egualmente ad assegnare un solo pitch, che per lo più corrisponde al tono fondamentale dell'insieme di parziali. Attenzione, ciò è vero quand'anche, nell'insieme di frequenze, quella fondamentale si trovasse a mancare (nel qual caso il pitch sarebbe del tutto virtuale).           

Sono stati formulati svariati modelli psicoacustici per spiegare tale comportamento, che tuttavia si riducono essenzialmente a due punti di vista: il cervello estrae il pitch analizzando la configurazione complessiva di deformazione della membrana basilare (modelli posizionali o tonotopici), in sostanza operando, per quanto detto sopra, un'analisi spettrale del suono; oppure analizza e giudica la successione nel tempo del treno di impulsi evocati sulla membrana basilare (modelli temporali o di periodicità).
Nessuno dei due tipi di modelli, da solo, spiega appieno i dati sperimentali, ma il secondo gode oggi di maggior credito; tuttavia è assai probabile che esso non operi mai disgiunto dal primo, altrimenti non si spiegherebbe l'indipendenza della percezione dei caratteri essenziali del suono - timbro, altezza, intensità - dalla fase delle parziali, circostanza che lascia supporre un'analisi spettrale del segnale globale.

V. IL CERVELLO DEVE POTER CONTARE

Esiste una teoria che compendia i due approcci,[12] giungendo a formulare la successione temporale degli impulsi neurali che raggiungono il cervello per i vari possibili tipi di stimolo, note e accordi musicali.
Come abbastanza prevedibile, essa corrisponde in buona misura all'andamento nel tempo dell'intensità dello stimolo sonoro; di più, essa si modella sull'andamento che tale intensità avrebbe se tutte le parziali raggiungessero il timpano in coincidenza di fase.[13]
Tale intensità, facilmente calcolabile, è mostrata in Fig. 7 per i principali intervalli musicali, dal consonante per antonomasia, la quinta perfetta do-sol, ad uno altamente dissonante, la settima maggiore do-si. Si osservano picchi dominanti e con marcata periodicità soltanto per gli accordi consonanti.

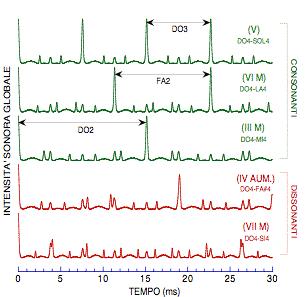
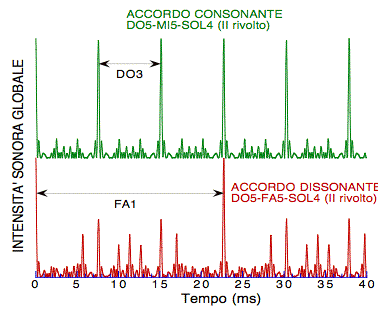
Fig. 7. Andamento nel tempo dell'intensità sonora di vari accordi diadici, da molto consonante a molto dissonante. Le singole note sono costituite da 9 armoniche di ampiezza decrescente in ragione inversa del numero d'ordine. Dall'alto in basso: quinta perfetta, sesta maggiore, terza maggiore, quarta aumentata (tritono), settima maggiore.

 In sintesi, il cervello deve avere la possibilità di "contare" per poter assegnare al suono complesso unitarietà, ossia omogeneità e fusione, e soprattutto pitch e timbro (oltre che per stabilirne il livello di intensità, come detto poc'anzi, benché a questo aspetto non mi sia potuto addentrare per ragioni di spazio). Ecco allora che l'affermazione di Leibniz, benché riferita con tutta probabilità al tempo musicale e al ritmo, va ben al di là delle intenzioni e acquista il sapore di geniale intuizione!

VI. CONCLUSIONI

  Quello che oggi sappiamo è che la possibilità di contare sta alla base della sensazione di consonanza e della percezione di una stoffa timbrica omogenea e compatta. Si potrebbe dire che i segnali classicamente consonanti sono preferiti perché più facili da elaborare per il sistema orecchio-cervello. Il conteggio è tanto più agevole quanto più il suono presenta una strutturazione armonica, sia quando è costituito da una nota isolata, sia quando risulta da un insieme di note. Il che non deve sorprendere, per il fatto che la strutturazione armonica è tipica dei suoni naturali, in primo luogo la voce umana, e quindi suscita configurazioni di eccitazione familiari al cervello.
In più, il riconoscimento dell'altezza, del timbro, dell'intensità sonora è stato attraverso i millenni una primaria necessità dell'uomo, che si è trovato ad avventurarsi in ambienti ostili giovandosi di tutti i suoi strumenti percettivi, in primis la vista e l'udito. E ciò ha reso tali attitudini - ripeto, il riconoscimento dei parametri caratterizzanti del suono - una fonte di soddisfazione, ed è stato forse la causa prima dell'arte di fare musica.

Queste considerazioni spingono a porre alcune domande circa i futuri sviluppi della musica. Negli ultimi due secoli, il gusto musicale si è grandemente evoluto rispetto ai canoni dell'armonia classica. La dissonanza negli accordi ha avuto l'effetto di esaltare la consonanza, introducendo nella musica qualcosa di equivalente al chiaroscuro in pittura; dissonanza e consonanza si sono integrate in un tessuto musicale più composito e spesso.
La timbrica si è molto ampliata, prima con l'avvento di strumenti con suono a strutturazione parzialmente inarmonica (tipico esempio la famiglia degli xilofoni, le percussioni e le campane tubolari), poi degli strumenti sintetici. E fin qui il pubblico non ha avuto soverchia difficoltà a "maturare" per l'occorrenza i propri meccanismi cerebrali.
Taluni più recenti tentativi di innovazione, di fronte ai quali le platee si mostrano riluttanti, potrebbero non aver tenuto nel debito conto le oggettive esigenze, le capacità e soprattutto gli eventuali limiti del sistema della percezione uditiva: vale a dire le condizioni imposte dai meccanismi fisici e fisiologici delle parti vibranti, le limitazioni dettate dai processi di decifrazione a livello psichico, e infine i problemi di assuefazione a suoni o a loro insiemi che non hanno un corrispettivo nella natura.

Circa il futuro della musica colta, chiudo con una frase ammonitrice di John Pierce:
«Per aver successo la nuova musica deve però essere sentita secondo le intenzioni del compositore, deve essere compresa, deve mantenere l'interesse e commuovere l'ascoltatore. A questo livello lo studio e l'esplorazione della scienza del suono musicale può essere d'aiuto. Ma il resto dipende solo dal talento e dal genio».
Altrimenti potrebbe aver ragione un illustre amico e collega che afferma:
«La buona musica - quella che si può apprezzare senza dover leggere le istruzioni per l'uso - è una dote che si è perduta».