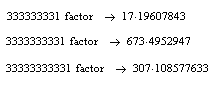
Metodo induttivo e deduttivo
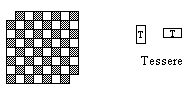
Sia abbia una tastiera mozza e un numero sufficiente di tessere che coprono due celle come in figura.

Di debba risolvere il seguente quesito:
E’ possibile coprire tutta la scacchiera usando le tessere in modo opportuno ?
Il problema può essere affrontato in due modi distinti.
1) Metodo induttivo.
Si prova a mettere le tessere sulla scacchiera e se non si riesce si riprova una strada diversa dalla precedente.
Dopo centinaia o migliaia di tentativi falliti si può dire che:
Tutte le prove finora eseguite mi inducono a credere che non si possono coprire tutte le caselle
della scacchiera con le tessere che coprono due celle. Naturalmente non si ha la certezza che il problema sia insolubile. Posso non avere sperimentato il caso favorevole.
In conclusione, il metodo induttivo fornisce la "verità" di una affermazione fino a che non si
trova una prova contraria.
Tutte le scienze sperimentali si basano sul metodo induttivo.
2) Metodo deduttivo
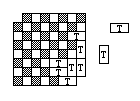
Si consideri il numero delle celle nere e di quelle bianche
![]()
Ogni tessera deve coprire un quadrato bianco e uno nero. Essendo il numero delle celle bianche diverso dal numero delle celle nere, si deduce che non si riuscirà mai a coprire tutta la scacchiera.
Si è ottenuta la certezza del risultato senza alcuna prova ma attraverso un ragionamento logico conseguenza delle premesse.
L’unica scienza che usa solo il metodo deduttivo è la matematica. La verità non scaturisce da prove ma da dimostrazioni.
In realtà, nelle scienze sperimentali, se ci si limitasse ad eseguire delle esperienze, non si andrebbe molto lontano. Ci vorrebbero decenni o centinaia di anni di prove ed errori per ottenere dei risultati.
Conviene creare un modello matematico di ciò che interessa e, con il metodo deduttivo ricavare dei risultati teorici e verificare in sede sperimentale l’attendibilità. Se i risultati non combaciano con la teoria si cambiano le ipotesi iniziali e si crea un nuovo modello matematico.
Altro quesito da risolvere
Vengono fornite delle coppie di numeri legate da una certa relazione. Bisogna trovare la relazione esistente.
![]()
Ci sono molte relazioni che possono risolvere il problema:
![]()
Non sapendo quale scegliere aspetto che venga fornita un’altra coppia di numeri.
![]()
Ancora ci sono molte relazioni che risolvono il problema
![]()
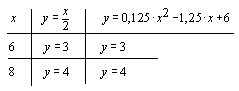
Non sapendo quale scegliere chiedo che mi venga fornita un’altra coppia di valori.
![]()
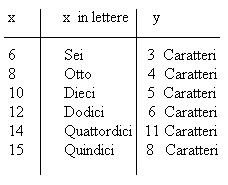
Ora scrivo tutte le coppie sotto forma di tabella:

Osservo che x è il doppio di y.
![]()
Questa è la relazione che sembra esserci tra x e y. Per confermare la teoria chiedo che
venga fornita un’altra coppia di numeri.
![]()
A questo punto sembra che la teoria sia corretta e chiedo un’altra coppia di valori per rinforzare
![]()
![]()
Questi valori fanno "crollare" l’ipotesi iniziale.
La teoria deve essere abbandonata.
Il legame tra x e y non è quello che sembrava.
La soluzione è: y indica il numero dei caratteri scritti in lettere.
Altro esempio di induzione "pericolosa"
Si consideri il numero 31 che è un numero primo.
Si aggiunga un tre a sinistra e si ottiene 331 che è ancora un numero primo.
Se si procede come nel caso precedente si ottengono ancora numeri primi.
I risultati sono ottenuti con l’aiuto di Mathcad.

Ragionando induttivamente si potrebbe dire che anche il numero 333 333 331 sarà un
numero primo.
Per affermare quanto sopra ci vorrebbe una dimostrazione ( metodo deduttivo ).
In realtà il numero 333 333 331 non è primo perché è divisibile per 17