Supponiamo che

1.0) ( a ° a ) = a + F(2)

che possiamo leggere: a con a uguale….

e generalizzando

1.1) ( a ° a ° a …. ° a ) = a + F(n)

dove n è il numero di volte che si ripete a

si avrà allora

1.2) ( a ° a ° a ) ° ( a ° a ° a ) = a + F(6)

che si può riscrivere così

1.3) [ a + F(3) ] ° [ a + F(3) ] = [ a + F(3) ] + F(2) = a + F(3) + F(2)

dove

1.4) a + F(3) + F(2) = a + F(6)

quindi

1.5) F(3)+F(2) = F(6)

che è un'eguaglianza isomorfa rispetto allo sviluppo del prodotto logaritmico !

infatti

log 3 + log 2 = log (3 * 2)

dunque

a ° a = a + log 2

in generale si ha

a ° a ° a ….. ° a = a + log n

Si può dimostrare che

1.6) a ° b = a + log [ 1 + e^(b-a) ]

e si può anche dimostrare che

1.7) log ( a + b ) = log a ° log b

Ora possiamo svolgere il logaritmo di una equazione di 2 grado

Poniamo di avere:

1) ax² + bx = c

il logaritmo di questa somma è:

2) 2x₁+a₁ ° x₁+b₁ = c₁

dalla 1.6) otteniamo

2x₁+a₁ ° x₁+b₁ = 2x₁ + a₁ + log [ 1 + e ^{(b1-a1 - x1)} ] = c₁

oppure

2x₁+a₁ ° x₁+b₁ = x₁ + b₁ + log [ 1 + e ^{(a1- b1 + x1)} ] = c₁

da cui si può ricavare una soluzione approssimata della x se a₁ >> 1 e a₁>> b₁ e c1>a1

x₁ + b₁ + a₁ - b₁ + x₁ = c₁

cioè

2x₁ + a₁ = c₁

quindi

x₁ = (c₁ - a₁) / 2

pertanto x sarà uguale a

x = e^{(c1 - a1) / 2}

dove e è la base del logaritmo.

Abbiamo ottenuto una soluzione di una particolare equazione di secondo grado, ma cosa si può dire del caso più generale?

E' utile a questo punto ricavare le curve della 1) e 2)  

Fig 1

La linea blu deriva dalla 1) quella rossa è il suo logaritmo e rappresenta la 2). Ora è chiaro che la 2) si può approssimare ad una retta, (il valore massimo raggiunto dalla y nella curva blu è 100000).

Da quanto detto, risulta che possiamo scrivere una funzione lineare che rappresenta un'approssimazione della 2)

3) c₁ = p₁ x₁ + k

assegnando due valori qualsiasi alla x della 1) e chiamando y il risultato si avrà

y₁ = p₁ x₁ + k

y₂ = p₁ x₂ + k

in cui y₁ , y₂ , x₁ ed x₂ sono i logaritmi di x ed y e da qui ricaviamo le costanti p₁ e k

p₁ = (y₂ -y₁) / (x₂ -x₁)

k = y₁ - p₁ x₁

pertanto ora che abbiamo tutti i valori richiesti, dalla 3) si ricava

x = e^{(c1-k / p1)}

Questo risultato è tanto più importante quanto maggiore è il grado dell'equazione, perché si può adottare lo stesso criterio per qualsiasi grado della principale.

Vedremo ora come si può ottenere una dimostrazione utilizzando Excel

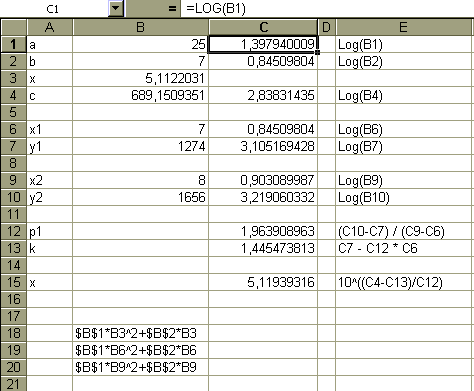
Fig 2

A beneficio di coloro che non conoscono Excel indichiamo passo, passo la procedura da seguire.

Si fa notare che scrivendo LOG, Excel usa il logaritmo in base 10. Inseriamo dei valori a piacere, purché positivi, nelle caselle B1, B2 , B3, B6 , B9

Nella casella B4 copiamo la formula che troviamo in B18, preceduta dal segno = , ora si copia Il contenuto della B4 e lo si incolla in B7 e B10 ottenendo automaticamente le formule di B19 e B20, ora le formule che compaiono nella colonna E si copiano nella colonna C, sempre precedute dal segno =.

Così facendo valutiamo l'equazione ax² + bx = c

In B3 abbiamo inserito il valore di x ed in C15 otteniamo il primo risultato approssimato della nostra equazione, ora copiamo il valore in C15 e con incolla speciale, dal menu Modifica, inseriamo il valore, (attenzione il valore, non la formula) alternativamente in B6 e in B9, ripetiamo questa operazione finché non otteniamo in C15 lo stesso risultato presente in B6 o B9, questo ci assicura che di aver trovato il valore di x. Per fare delle prove sul funzionamento dell'algoritmo possiamo inserire il valore di x nella casella B3 e ricavare il valore di c nella casella B4, però normalmente x non è noto, al contrario è noto c, quindi se si conosce c, allora in B4 inseriamo il valore di c, e come si è già detto, per essere sicuri di aver trovato x basta controllare che coincidano di C15 con B6 o B9. In ogni caso le caselle B7 e B10 dovranno contenere le equazioni B19 e B20 precedute dal segno uguale.

Noteremo che si raggiungerà molto presto lo scopo perché la funzione è rapidamente convergente. Questo è un altro punto notevole della soluzione proposta con la nuova operazione.

Come si è detto il metodo vale per un'equazione di grado qualsiasi, come ulteriore esempio inseriamo un foglio di excel per l'equazione di 5° grado che come è noto non è risolvibile.

Fig. 3

In figura 3, l'algoritmo da usarsi per risolvere l'equazione di 5° grado. Le equazioni che compaiono nella colonna E vanno copiate nella colonna C, quelle in B20, B21, B22 vanno copiate rispettivamente nelle caselle B7, B10, B13.