Le equazioni e disequazioni irrazionali

Teoria in sintesi

EQUAZIONI IRRAZIONALI

Un'equazione è irrazionale se contiene almeno un radicale nel cui radicando compare l'incognita.

Ad esempio

, è un'equazione irrazionale;

, non è un'equazione irrazionale.

Data un'equazione A(x)=B(x), consideriamo l'equazione :

· se n è pari, essa ha come soluzioni, oltre a quelle di A(x)=B(x), anche quelle di A(x)=-B(x);

· se n è dispari, essa è equivalente a quella data.

N.B.: Prova a risolvere la seguente equazione

e l'equazione

Si ottengono le stesse soluzioni? Le due equazioni sono equivalenti?

[La prima equazione dà come soluzione , la seconda invece ]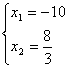

Per risolvere un'equazione irrazionale

è necessario "liberarci" in qualche modo dei radicali presenti, per ricondurre il problema alla soluzione di una equazione razionale che ci dia buone informazioni sulle soluzioni dell'equazione iniziale. Per fare questo operativamente dobbiamo:

· elevare a n entrambi i membri dell'equazione;

· controllare se n è pari o dispari: se n è dispari, le soluzioni dell'equazione ottenuta sono le stesse dell'equazione irrazionale; se n è pari, possiamo eseguire il controllo delle soluzioni mediante verifica.

Esempio

Elevando entrambi i membri al quadrato otteniamo

che ci dà come soluzione .

Questi valori saranno anche soluzione dell'equazione di partenza?

Per verificarlo sostituiamo 7 e 2 nell'equazione irrazionale data.

Sostituiamo x=7

Primo membro Secondo membro

Ora sostituiamo x=2

Nel secondo caso, poiché i due membri dell'equazione non hanno lo stesso valore, la radice x=2 non è soluzione dell'equazione irrazionale.

N.B.: C'è un altro metodo per verificare quali soluzioni sono accettabili? Si, bisogna imporre la non negatività del radicando e del secondo membro, ottenendo così la condizione …..Controlla tu!

DISEQUAZIONI IRRAZIONALI

Le disequazioni irrazionali del tipo sono equivalenti a un sistema di tre disequazioni:

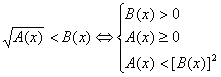
Mentre le disequazioni irrazionali del tipo hanno come insieme di soluzione l'unione degli insiemi delle soluzioni di due sistemi, ognuno di due disequazioni:

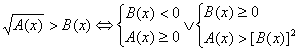
Esempio

(oppure )

La disequazione ha senso quando

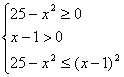
N.B.: La prima condizione è necessaria perché esista la radice, la seconda perché se la disuguaglianza in questione non sarà mai verificata (perché si chiede che una quantità positiva al primo membro sia di una quantità negativa al secondo membro!).

Si ottiene quindi, dopo brevi passaggi,

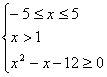
Le soluzioni accettabili sono quindi .

Potrebbe essere utile provare a fare i grafici di

per capire la discussione algebrica del sistema.

Esercizi

1. Risolvere le seguenti equazioni irrazionali, controllando l'accettabilità delle soluzioni.

[Perché la soluzione non è accettabile?]

[0; -4]

[-5]

[Perché la soluzione non è accettabile?]

(dopo aver elevato al quadrato due volte, si ottiene ….)

[0; ]

2. Risolvere le seguenti disequazioni irrazionali, seguendo lo schema di teoria in sintesi per verificare l'accettabilità delle soluzioni, ed aiutandoti con il grafico.

N.B.: il grafico riassuntivo di questa disequazione irrazionale è il seguente

-1 0