SUDOKU
QUICK COURSE
(from the SUDOKU
PERSONAL TRAINER v 2.2 program help file)
Copyright © Giorgio
Altichieri - 10/2007
INTRODUCTION
Sudoku is a puzzle,
to be solved logically.
Its most common Scheme consists in 81 Cells laid out on a grid (or table)
with 9 Rows and 9 Columns; the Scheme shows also, by
more evidenced borders, 9 Boxes of 3 x 3 Cells each (also called Blocks or Regions).
The puzzle starts with the numbers (1 to 9) in some
Cells only; to solve the puzzle the player must fill the empty Cells with those
numbers, respecting the Base Rule that “each Row, Column
and Box must contain each number 1 to 9
exactly once”.
Figures and samples
you find here come from the SUDOKUPTI (Sudoku Personal Trainer
v 2.2) program
that offers an environment that helps
the player to solve the 81 Cells Sudoku and that at the same time may drive
beginners and less experienced payers,
suggesting each move, while its logical motivation lets the opportunity for learning
techniques and typical tricks.
TERMINOLOGY
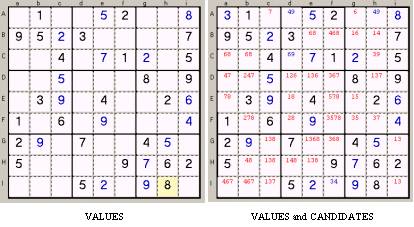
- Row, Column, Box, Cell: as defined above;
- Zone: means a
Row, a Column or a Box indifferently;
- Value: is a
number (1-9) present in a Cell, or from the beginning or played during the
game (the initial Values are black, the
played ones are blue);
- Candidates:
are all the allowed Values you can play in a Cell, in respect of the Sudoku
Base Rule. Since every new move adds a new Value it should force the player to
do new reasoning, but that is done by the program (the Candidates that are
automatically calculated in this way are red, while those adjusted directly by
the player are blue);
- Exclusions:
are all not admitted Values in a Cell,
because conflicting with the Sudoku Base Rule;
- Double: if a
Cell admits only two Candidates that is a Double;
- Conjugated Pairs: when, during the game, a Candidate appears
(alone or with some others) only in one Cell of a Zone (for instance a Column), then it is certainly true and it is the Value to be assigned
to that Cell. But if it is present in
two Cells of a Zone, it realises a Conjugated Pairs that have the propriety
that the above Candidate will be true in a Cell and false in the other;
- Twins: (not to
be confused neither with Double nor with Conjugated Pairs) you have Twins when in a Zone two Cells
accept the same two Candidates. Twins can be “naked” (pure, and you have two
equal Doubles), or “hidden” when some other Candidate appears in one or both
those Cells;
- Triple: as
above when there are three Cells which share in any way the same 3 Candidates;
- Quad: as above
when there are four Cells which share in any way the same 4 Candidates.
At
large, a given set of numbers on a Sudoku Scheme can:
- have no Solution;
- accept only one Solution: that is the case
of those you find on papers and magazines;
-
accept more than one Solution: in this case the Sudoku program follows
the one it finds first.
Some Schemes can be
solved without Candidates' evidence (I call this way “at a glance”). Very
often, anyway, after a first set of Moves, it becomes necessary to write the
Candidates into their Cells for appropriate reasoning. The program let you work
in both ways, passing from one to the other at any time you want: in fact a Move
you discover with Candidates put in evidence may take back the opportunity to
play new simple Moves "at a glance".
There is a set of “logical Methods”
(reasoning or techniques) to play the Moves.
Those rational constructions are sufficient to solve the Sudoku Schemes
you find on general daily and magazine game pages. However, on Sudoku specialised magazines or Internet pages you
can find Schemes where, after having used all available rational methods, you
must proceed “by Trials”.
The SUDOKUPTI program offers the environment that helps you to play that way,
as well.
METHODS (OR TECHNIQUES)
METHOD 1 - At a glance: by crossing Rows/Columns/Boxes with the
same Value (1-9), you find that some Zone remains with just one
not-excluded Cell (the Method may be known as “slice and dice”). Easy
Sudokus might be entirely solved with this Method.
 Sample 1a -
Crossing Rows and Columns having the 5 Value, happens that in the marked Box
only the azure Cell can accept that Value.
Sample 1a -
Crossing Rows and Columns having the 5 Value, happens that in the marked Box
only the azure Cell can accept that Value.
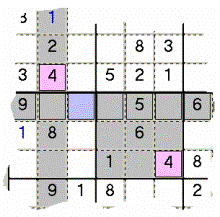 Sample 1b - It is the same case when the target
Zone to cross is a Row. The central grey Box, with its pink 4 Value, forbids 4
in the empty Cells shared with the grey Row. The grey Column, with its pink 4
Value, forbids 4 in the Cell shared with the grey Row: if the grey Row (here
not entirely shown) does not have other free Cells, only the blue Cell can
receive 4 as Value.
Sample 1b - It is the same case when the target
Zone to cross is a Row. The central grey Box, with its pink 4 Value, forbids 4
in the empty Cells shared with the grey Row. The grey Column, with its pink 4
Value, forbids 4 in the Cell shared with the grey Row: if the grey Row (here
not entirely shown) does not have other free Cells, only the blue Cell can
receive 4 as Value.
METHOD 2 - Only one
missing Cell to complete a Zone (Single Cell).

Sample 2 - in the marked Row, only the azure Cell has to be done so you
can confirm 2 there.
METHOD 3 - Only one
Candidate in a Cell (Single Number).

Sample 3 - The azure Cell admits only one Candidate, so you can confirm it.
METHOD 4 - A Zone shows
a certain Candidate in one Cell only, but it is accompanied by some other
Candidate (Hidden Single
or hidden loner).
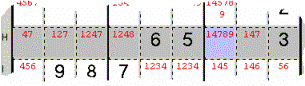
Sample 4 - In Row H the Candidate
9 exists only in the azure Cell (even if accompanied by others
Candidates) so you can confirm 9 there.
METHOD 5 - A Zone
shows exact Twins Candidates, i.e. the
same pure Double appears twice (Naked Twins or pure twins).
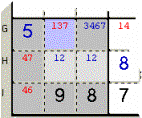
Sample 5 - In the marked Zone there are two Twins (the two Cells with
the Double 12 in pale grey). Using only
two Candidates, here 1 and 2, you
cannot satisfy any other Cell, so the 1
appearing in the azure Cell must be cancelled from there.
METHOD 6 - A Zone
has two Cells with the same double of Candidates, but one double or both are accompanied by other Candidates (Hidden Twins).
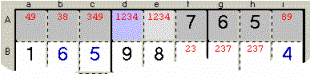 Sample 6 - The Row A shows only two Cells
with the Candidates 1 and 2, but accompanied by others Candidates. On two
Cells you cannot play more than two Candidates, and since they appear only there
you must cancel every different one. In this example the PERSONAL TRAINER says
to liberate the azure Cell, but obviously you should clean up also the second
Cell interested by these Twins (marked in pale grey).
Sample 6 - The Row A shows only two Cells
with the Candidates 1 and 2, but accompanied by others Candidates. On two
Cells you cannot play more than two Candidates, and since they appear only there
you must cancel every different one. In this example the PERSONAL TRAINER says
to liberate the azure Cell, but obviously you should clean up also the second
Cell interested by these Twins (marked in pale grey).
METHOD 7 - A Box
locks a Candidate on a Row or Columns of
its, but that Candidate appears on the same Row or Column also outside
that Box (Box Locks
Candidate).
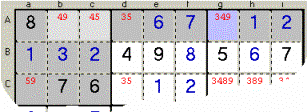
Sample 7 - The Box ABCabc
foresees the Candidate 4 (pale grey Cells) only on its part of Row A; it will
surely go there, but, since the same A Row shows the Candidate 4 also (azure
Cell) outside that Box, the 4 must be
cleaned up from there.
METHOD 8 - A Row or
Column locks a Candidate in one Box only, but the Candidate appears also in
other Cells of that Box (Row/Col. Locks Candidate).
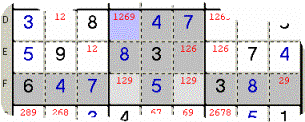
Sample 8 - The Row F foresees
the Candidate 1 only within the marked Box; the Candidate 1 will surely be true
in one of the pair of those pale grey Cells,
as a consequence it cannot be accepted in any other Cell of the same Box
(not in the azure one; note that there is another Cell to clean but the program
is suggesting the first now).
METHOD 9 and 10 - 3
(o 4) Cells of a Zone admit just all or some of the same 3 (or 4) Candidates,
but those Candidates appear even in one or more other Cells of that Zone (Candidates Sharing).
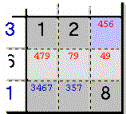
Sample 9 - Using only three
Candidates you cannot satisfy more than three Cells of the same Zone. It
happens here for the marked Box and its three pale grey Cells, showing 4, 7 and 9; as a consequence you can
clean up 4 from the azure Cell (note that are other Cells to clean but the
program is suggesting the first now).
 Sample 10 - Using
only four Candidates you cannot satisfy more than four Cells of the same Zone.
It happens here for the marked Row and its four pale grey Cells showing 2, 3, 8
and 9; as a consequence you can clean up 8 and 9 from the azure Cell.
Sample 10 - Using
only four Candidates you cannot satisfy more than four Cells of the same Zone.
It happens here for the marked Row and its four pale grey Cells showing 2, 3, 8
and 9; as a consequence you can clean up 8 and 9 from the azure Cell.
METHOD 11 - A Zone
shows 3 Cells with exactly the same three Candidates, that appear also in some
other Cell of its (Naked Triples or pure
triples).
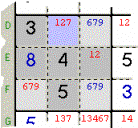
Sample 11 - In the marked Zone there are three pure Triples (the three
Cells in pale grey with the Triple 679
). Those Candidates cannot be true in any other Cell of the same Zone, so you
can clean up 7 from the azure Cell.
METHOD 12 - A Zone
shows 3 Cells with the same three Candidates, ma some other Candidate accompany
them in those Cells (Hidden Triples).
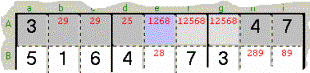
Sample 12 - In the A Row, the three marked Cells (azure and pale grey)
hide the Triple 168; you can start cleaning up 2 from the azure Cell, and then
clean up conveniently the other two pale grey Cells to leave only 168 in each
of them.
METHOD 13 - The Scheme shows
an X-Wing Rectangle. When two Rows shows the
same Conjugated Pair and those Cells belong to the same two Columns (those four
Cells form a rectangle), then every other presence of that Candidate on those
Columns is certainly false.
The same can be said switching
Rows and Columns, when the above Conjugated Pairs lay on Columns.
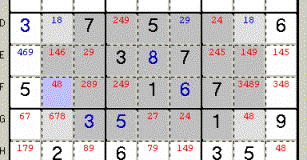
Sample 13 - The Candidate 8
appears on the corners of a X-Wing Rectangle, based on D and G Rows having just
those 8 as Conjugated Pairs;
accordingly the theory the 8 Candidate is admitted only on the rectangle’s
corners, but not in other points of its
sides or of its sides’ continuations;
as a consequence you can clean up the azure Cell of the second Column.
METHOD 14 - The
Scheme shows a SwordFish Butterfly.
When 3 Rows shows 2 or 3 Cells with the same Candidate and those Cells lay on
the same 3 Columns (so that you can see
two partially overlapping rectangles, just about two butterfly’s wings), then
every other presence of that Candidate on those Columns is certainly
false. The same can be said switching
Rows and Columns.
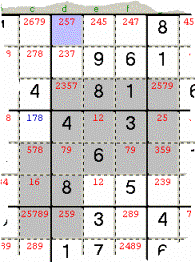
Sample 14 - The Candidate 5
realises a Swordfish Butterfly lying on three Rows (the horizontal sides of two
Rectangles with an overlapped corner showing 79, as the Butterfly centre); accordingly the theory you can cancel
the Candidate 5 outside the corners, if
it appears somewhere else on the Columns of the three vertical rectangle sides;
that is the case of the azure Cell.
METHOD 15 - A Zone shows 4
Cells with exactly the same four Candidates, that appear also in some other
Cell of its (Naked
Quads or pure quads).
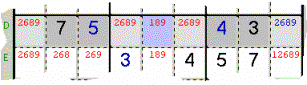 Sample 15 - In the
Row D the Quad 2689 appears exactly four times, in the pale grey Cells. But the
azure Cell shows the Candidates 89
already necessary for the Quad itself,
as a consequence you can clean them up from the azure Cell.
Sample 15 - In the
Row D the Quad 2689 appears exactly four times, in the pale grey Cells. But the
azure Cell shows the Candidates 89
already necessary for the Quad itself,
as a consequence you can clean them up from the azure Cell.
METHOD 16 - A Zone shows 4
Cells with the same four Candidates, ma some other Candidate accompany them in
those Cells (Hidden Quads).
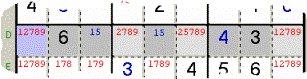 Sample 16 - In the
Row D there are four Cells (in pale grey and azure) having the Quad 2789, but
somewhere those Quads are not pure. You can clean them up from any unwanted
Candidate, maybe starting taking away 1 in the azure Cell and then the cleaning
up the others as necessary.
Sample 16 - In the
Row D there are four Cells (in pale grey and azure) having the Quad 2789, but
somewhere those Quads are not pure. You can clean them up from any unwanted
Candidate, maybe starting taking away 1 in the azure Cell and then the cleaning
up the others as necessary.
METHOD 17 – When none of the
previous methods can be used, the player must proceed by Trial, that is “Try and error”:
assume that a certain Candidate is the true Value and see what the hypothesis
generates.
Two remarks:
- “Trying” with pencil, paper
(and rubber) might be very complex;
- Playing with “Trials” isn’t
cheating, because it requires co-ordination and cleverness.
When in “Trial Mode” the
program temporarily hides all the Values and switch to an environment where the
player may choose a Cell, a starting Candidate and trigger a step by step try
process. The program offers two ways: trying seeing All
the current Candidates or only those achieving some Conjugated
Pairs (see TERMINOLOGY)..
HOW TO USE THE PERSONAL TRAINER
 When the player
does not find a right Move to continue the game or when he wants to go faster,
he can appeal to the PERSONAL TRAINER (or Teacher). The PERSONAL TRAINER gives
his Advice accordingly to the standard Priority or the Priority the player can
modify from the “Tools” menu.
When the player
does not find a right Move to continue the game or when he wants to go faster,
he can appeal to the PERSONAL TRAINER (or Teacher). The PERSONAL TRAINER gives
his Advice accordingly to the standard Priority or the Priority the player can
modify from the “Tools” menu.
Who really wants to learn, should ask him respecting the following
gradual stages:
- “Method” button: it prompts on the
blackboard the most convenient Method in that moment and this information may
be enough for the player to proceed autonomously;
- “Value“
button (to be used if the “Method” button does not solve enough):
it appends on the blackboard another line saying what to write or cancel on the
Scheme; even if the interested Cell is not mentioned yet, the information may
light the way to the right Move;
- “Where”
button (to be used if it’s still too dark!):
keeping it pressed you can identify on the Scheme the Cell to write into (azure
background), other Cells that are interested by the suggested Method (grey
background) and other possible Cells to consider (maybe with pink background o
a pale-grey one).
When releasing the “Where” button the coloured backgrounds disappear and
only the Cell to play into keeps the evidence with its yellow background and
can be manually played, but for the laziest …
- “Do
it” button (or F2): can make the program itself
to write the Move.
THE NETS
A Candidate’s Net is the drawing
obtained joining with horizontal and vertical lines all the Cells that at that
moment allow the Candidate. Reasoning on the Nets’ shapes may help to play some correct Move.
The SUDOKUPT program, as said before, offers among the “Advanced
Functions” the Nets viewing.
Here you find some Net patterns: they are real cases, the program has
produced.
Normally the Candidates are represented with an empty circle, but if from the “View” menu the choice “Show Solution” has been selected, a filled circle is used for “true” Candidates; this is the case of the samples below, but don’t overrate empty or filled, because those depended from the specific underlying game. Pay attention to the comments, instead.
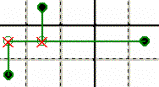
FREE BRANCHES – The “ends” are surely true, the
“nodes” false.
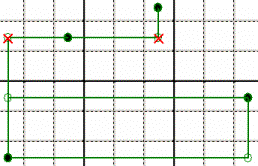
GRAFTED BRANCHES – Starting from a free “end” (that is
true, as said before) you can assume sequences of false/true “nodes”.
 SIMPLE RECTANGLE
– One couple of opposite corners is true, the other is false: it depends on the
specific game. The Simple Rectangle a the bare figure that can complicate
itself in many ways (to become, maybe, the X-WING following here).
SIMPLE RECTANGLE
– One couple of opposite corners is true, the other is false: it depends on the
specific game. The Simple Rectangle a the bare figure that can complicate
itself in many ways (to become, maybe, the X-WING following here).
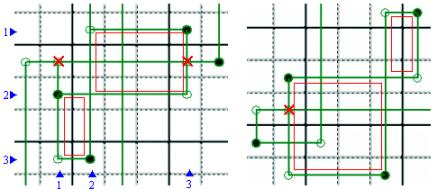
 X-WING – It occurs when two Rows (or two
Columns) contain the subject Candidate only twice and in such a way that those
Cells are the corners of a Rectangle. If that occurs, then all other instances
of the subject Candidate outside its corners are surely false. As for true Candidates:
it depends on the game.
X-WING – It occurs when two Rows (or two
Columns) contain the subject Candidate only twice and in such a way that those
Cells are the corners of a Rectangle. If that occurs, then all other instances
of the subject Candidate outside its corners are surely false. As for true Candidates:
it depends on the game.
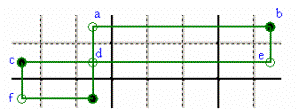
TWO CORNER-JOINED RECTANGLES – One of three
combination is true: aef, bcg, bdf.
When the d Candidate is missing, you must consider only aef, bcg
combinations. (This is the base shape
that can origin a SWORDFISH pattern that follows here).
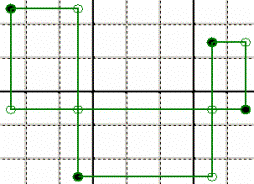
 SWORDFISH
- It occurs when three Rows (or three
Columns) contain the subject Candidate only twice in such a way that its Cells
lie on the same three Columns (or Rows) and those Cells are the angles of Two
Corner-Joined Rectangles. If that occurs, then all other instances of the
subject Candidate outside its corners are surely false. As for true Candidates:
it depends on the game.
SWORDFISH
- It occurs when three Rows (or three
Columns) contain the subject Candidate only twice in such a way that its Cells
lie on the same three Columns (or Rows) and those Cells are the angles of Two
Corner-Joined Rectangles. If that occurs, then all other instances of the
subject Candidate outside its corners are surely false. As for true Candidates:
it depends on the game.
Note – The same if
the Candidate exists in the joined corner Cell, as well. (three instances
on that Row/Column).
 MORE
CORNER-JOINED RECTANGLES - (with or not
the subject Candidate in the Corner-Join Cells) – Every combination of opposite corners might be true (one is shown
here).
MORE
CORNER-JOINED RECTANGLES - (with or not
the subject Candidate in the Corner-Join Cells) – Every combination of opposite corners might be true (one is shown
here).

NESTED RECTANGLES – There are three possible true
combinations (one is shown here).
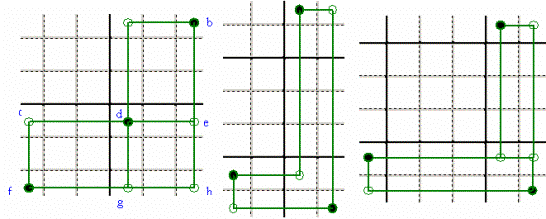
A SQUARE OF RECTANGLES – No exclusion a priori. Every
combination: ach, aef, bdf (here shown), bce might be true. Some Candidate
(like d e g h) may be missing.
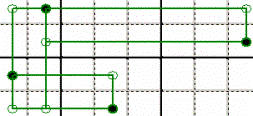 SQUARES
SEQUENCE – You can consider any opposite corners combination, beside the one
shown here.
SQUARES
SEQUENCE – You can consider any opposite corners combination, beside the one
shown here.
More information can be found
on the SUDOKUPTI Help file.
Have a nice fun!