CORSO RAPIDO DI SUDOKU

(Estratto dal file d’aiuto del programma SUDOKU PERSONAL TRAINER v 2.0)

Copyright © Giorgio Altichieri - 10/2007

INTRODUZIONE

Il Sudoku è un gioco solitario, da risolvere col ragionamento.

Lo Schema più diffuso consiste in una tabella di 81 Caselle (o celle) suddivise su 9 Righe e 9 Colonne; lo Schema mostra poi, con bordi più marcati, 9 Quadri di 3 x 3 Caselle contigue ciascuno (detti anche blocchi o regioni).

Per il gioco lo Schema mostra i numeri solo in alcune Caselle; il giocatore deve riempire le Caselle restanti coi valori da 1 a 9, rispettando la regola base (unica regola) che “ogni Riga, Colonna e Quadro contenga tutte le cifre da 1 a 9, senza ripetizioni”.

Le figure e gli esempi che seguono sono stati ottenuti col programma SUDOKUPT (Sudoku Personal Trainer v 2.0) che offre un ambiente che facilita la soluzione dei Sudoku di 81 Caselle e che su richiesta può suggerire la singola mossa, motivarla logicamente, favorendo così l’apprendimento delle tecniche e dei trucchi più tipici.

TERMINOLOGIA

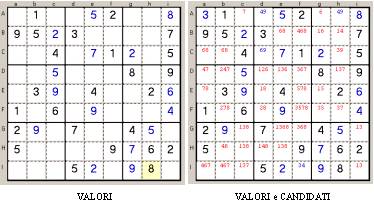
- Riga, Colonna, Quadro, Casella: già definiti più sopra;

- Zona: indica indifferentemente una Riga, una Colonna o un Quadro;

- Valore: è il numero (1-9) già presente in una Casella, fin dall’inizio, o giocato durante la partita (il programma mostra i Valori iniziali in nero, quelli giocati in blu);

- Candidati: sono i possibili Valori assegnabili a una Casella in un certo momento del gioco, nel rispetto della regola base. In certi momenti è inutile visualizzarli, in altri sono indispensabili per poter proseguire. Il programma li rappresenta con dei numeri più piccoli all’interno delle Caselle non ancora risolte (i Candidati calcolati automaticamente appaiono in rosso, quelli corretti manualmente sono in blu);

- Esclusioni: sono i Valori che una Casella non può accettare, perché violerebbero la regola base;

- Doppietta: se in un certo momento del gioco un Candidato compare (da solo o con altri) soltanto in una Casella di una certa Zona (ad esempio una Colonna), esso è certamente Vero ed è il Valore da dare a quella Casella. Se invece compare solo in due Caselle di una stessa Zona, costituisce una Doppietta che gode della proprietà che il Candidato sarà Vero in una Casella e falso nell’altra o viceversa;

- Coppia (da non confondere con la Doppietta): si ha una Coppia quando in una stessa Zona due Caselle accettano gli stessi 2 Candidati (es. due Caselle mostrano entrambe un 4 e un 7). Una Coppia può essere “nuda” o pura (es. 47 e 47), oppure “nascosta” per la presenza contemporanea di altri Candidati in una o in entrambe le Caselle (es. 47 e 2479);

- Terna: idem per tre Caselle di una stessa Zona con gli stessi 3 Candidati;

- Quaterna: idem per quattro Caselle di una stessa Zona con gli stessi 4 Candidati.

- Mossa del giocatore: può essere di due tipi, ossia o scrive il Valore in una Casella o sfoltisce i Candidati lì rimasti.

In generale una combinazione iniziale di numeri su uno Schema Sudoku può:

- non avere soluzione;

- avere una sola Soluzione e questo è normalmente il caso degli Schemi proposti sui giornali;

- avere più soluzioni: in questo caso il programma SUDOKUPT propone la prima che individua.

Alcuni Schemi possono essere risolti senza che sia necessario visualizzare e aggiornare i Candidati (chiamiamo questo modo “a colpo d’occhio”). Molto spesso però, dopo una prima serie di mosse, è indispensabile evidenziare i Candidati sullo Schema per ragionarci sopra. Il programma SUDOKUPT consente di lavorare nei due modi e, volendo, di passare da uno all’altro modo in qualunque momento, infatti una Mossa ragionata sui Candidati può riportare nello Schema la possibilità di successive semplici mosse “a colpo d’occhio”.

Esiste una serie di “Metodi logici”, ragionamenti o tecniche per giocare le mosse. Queste valutazioni razionali sono sufficienti per risolvere gli Schemi che trovate nelle pagine di passatempo dei quotidiani e dei periodici non specializzati. Nelle riviste e nei siti specialistici di Sudoku potete però trovare anche Schemi nei quali, una volta esauriti i metodi razionali, occorre procedere “per Tentativi”. Il programma SUDOKUPT offre anche l’ambiente specifico che aiuta in questa situazione.

I METODI

METODO 1 - A colpo d’occhio: incrociando Righe/Colonne/Quadri con uno stesso Valore (1-9), si trova che una Zona resta con una sola Casella non Esclusa (slice and dice). Negli Suddoku più semplici questo Metodo può portare da solo alla completa soluzione.

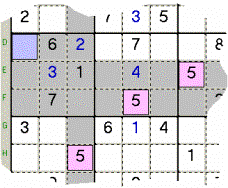Esempio 1a: incrociando Righe e Colonne col Valore 5, rimane nel Quadro mostrato in grigio solo la Casella azzurra che lo può accettare (notare che questo Metodo non utilizza la visualizzazione dei Candidati e che è molto conveniente per sgrossare il gioco, prima di ragionare sui Candidati).

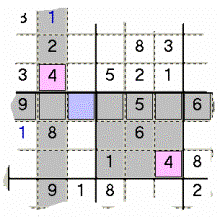Esempio 1b: è lo stesso Consiglio nel caso in cui la Zona che riceve gli incroci sia una Riga. Il Quadro centrale grigio, col suo Valore 4 rosa, rende escluse al 4 le due Caselle della Riga grigia ai lati del 5; la Colonna grigia, col suo 4 rosa, esclude la Casella sottostante in cui incrocia la Riga grigia: se la Riga grigia (qui non mostrata per intero) non ha altre Caselle libere, l’unica che può ricevere il 4 è quella azzurra.

METODO 2 - Manca una sola Casella per completare una Zona (single cell).

Esempio 2: nella Riga evidenziata in grigio manca solo la Casella azzurra e lì si può confermare il Candidato 2 che è proprio il Valore mancante alla Zona.

METODO 3 - Una Casella mostra un solo Candidato (single number).

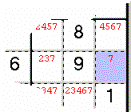
Esempio 3: si può confermare il Valore 7 nella Casella azzurra che ha solo un Candidato, appunto il 7.

METODO 4 - Una Zona mostra un certo Candidato in una sola Casella, ma altri Candidati lo nascondono (hidden loner o hidden single).

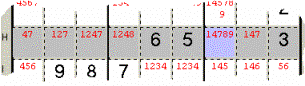
Esempio 4: nella Riga H il Candidato 9 è presente solo nella Casella azzurra (pur se mescolato con 1789) perciò lo si può confermare come suo Valore.

METODO 5 - Una Zona ha due Caselle con la stessa Coppia di Candidati che però appaiono in altre sue Caselle (pure pairs o naked pairs).

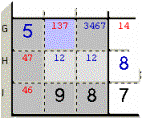
Esempio 5: nella Zona (Quadro) evidenziata ci sono due Caselle ‘Hb’ e ‘Hc’ con la Coppia pura 12 (grigio chiaro). L’ 1 e il 2 li devo giocare per forza lì anche se ancora non so esattamente come. Comunque, non posso soddisfare anche la Casella ‘Gb’ azzurra della stessa Zona, perciò da quella azzurra va tolto il Candidato 1.

METODO 6 - Una Zona ha due Caselle con la stessa Coppia di Candidati, ma altri Candidati l’accompagnano in una o in entrambe le Caselle (hidden pairs).

Esempio 6: la Riga A ha le Caselle ‘d’ e ‘e’ con la Coppia nascosta 12, nascosta dai Candidati 3 e 4 che l’accompagnano. L’ 1 e il 2 compaiono solo in ‘d’ e ‘e’, mentre il 3 e il 4 sono accettati anche in altre Caselle della Riga. Poichè in ‘d’ e ‘e’ non si possono giocare più di due Candidati, possiamo liberarle dal 3 e dal 4. Nelle Caselle ‘d’ e ‘e’ lasciamo solo la Coppia pura 12.

METODO 7 - Un Quadro imprigiona un Candidato su una sua Riga o Colonna, ma il Candidato appare sulla stessa Riga o Colonna al di fuori di quel Quadro (locked candidates 1).

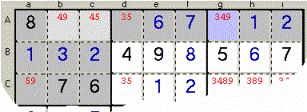
Esempio 7: il Quadro ‘ABCabc’ prevede il Candidato 4 (Caselle grigio chiaro) solo in corrispondenza della Riga A; lì il 4 vi andrà di sicuro, ma sulla stessa Riga A il 4 appare anche (Casella azzurra) al di fuori di quel Quadro, perciò da lì deve essere rimosso.

METODO 8 - Una Riga o una Colonna imprigiona un Candidato in un solo Quadro, ma il Candidato appare anche in altre Caselle di quel Quadro (locked candidates 2).

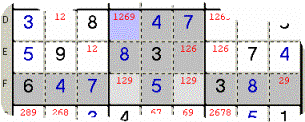
Esempio 8: la Riga F prevede il Candidato 1 solo dentro al Quadro evidenziato in grigio; l’ 1 andrà di certo in una delle sue due Caselle in grigio chiaro, perciò non potrà esserci in altre Caselle dello stesso Quadro (non in quella azzurra con 1269 e neppure nell’altra con 126).

METODI 9 e 10 - Solo 3 (o 4) Candidati soddisfano 3 (o 4) Caselle di una Zona, però appaiono anche in altre Caselle di quella Zona (number sharing).

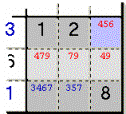
Esempio 9: coi tre Candidati 4, 7 e 9 nelle Caselle in grigio chiaro non posso soddisfare più di quelle tre Caselle dello stessa Zona (il Quadro), perciò devo togliere 4 dalla Casella azzurra con 456 e poi togliere 47 da quella con 3467 e poi levare 7 da quella con 357.

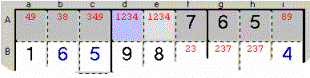
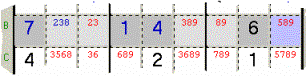Esempio 10: coi quattro Candidati 2, 3, 8 e 9 non posso soddisfare altre Caselle della stessa Zona (Riga B) oltre alle quattro in grigio chiaro, perciò devo togliere 8 e 9 dalla Casella azzurra.

METODO 11 - Una Zona ha 3 Caselle con la stessa Terna di Candidati, che però appaiono in altre sue Caselle (pure triples o naked triples).

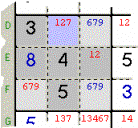
Esempio 11: nel Quadro evidenziato ci sono tre Caselle (grigio chiaro) con la Terna nuda 679. Tali Candidati non possono valere in altre Caselle della stessa Zona e devo togliere il 7 dalla Casella azzurra.

METODO 12 - Una Zona ha 3 Caselle con la stessa Terna di Candidati, ma altri Candidati li nascondono (hidden triples).

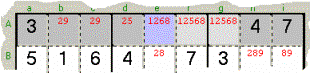
Esempio 12: nella Riga A, nelle tre Caselle evidenziate (azzurra e grigio chiaro), si nasconde la Terna 168; cominciamo ripulendo dal Candidato 2 la Casella azzurra, poi puliremo adeguatamente le altre due Caselle in grigio chiaro.

METODO 13 - Rettangolo X-Wing. Se due Righe hanno lo stesso Candidato in Doppietta e tali Caselle stanno sulle stesse Colonne (si forma appunto un rettangolo), allora sono certamente false tutte le altre presenze di quel Candidato su quelle Colonne.
Lo stesso si può dire invertendo Righe e Colonne se le Doppiette appartengono a quest’ultime (altri esempi più avanti il paragrafo dei RETICOLI).

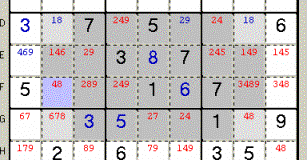
Esempio 13: il Candidato 8 si presenta ai vertici (grigio chiaro) del rettangolo X-Wing appoggiato sulle Righe D e G che hanno le Doppiette di 8. Secondo la teoria l’8 va ammesso solo ai vertici di tale rettangolo, perciò va tolto dalla Casella azzurra della Colonna di sinistra e da qualunque altra Casella delle Colonne sui lati (inclusi i loro prolungamenti).

METODO 14 - Farfalla SwordFish. Se 3 Righe mostrano 2 o 3 Caselle con lo stesso Candidato e tali Caselle stanno sulle stesse 3 Colonne (si formano due rettangoli parzialmente sovrapposti, quasi come le ali di una Farfalla), allora sono certamente false tutte le altre presenze di quel Candidato su quelle Colonne.

Lo stesso si può dire invertendo Righe e Colonne (altri esempi più avanti il paragrafo dei RETICOLI).

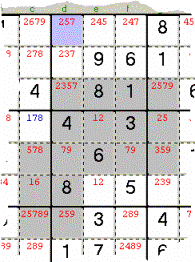
Esempio 14: il Candidato 5 configura una Farfalla Swordfish appoggiata su tre Righe (i lati orizzontali dei due Rettangoli col vertice sovrapposto dove c’è 79, centro della Farfalla); secondo la teoria si può togliere il Candidato 5 se appare sulle tre Colonne al di fuori dai sei vertici liberi ed è il caso della Casella in azzurro.

METODO 15 - Una Zona ha 4 Caselle con la stessa Quaterna di Candidati, che però appaiono in altre sue Caselle (pure quads o naked quads).

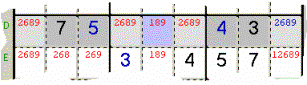
Esempio 15: nella Riga D la Quaterna 2689 si ripete quattro volte nelle Caselle in grigio chiaro. La Casella azzurra però propone anche i Candidati 89 che già sono impegnati a soddisfare la Quaterna, perciò vanno tolti dalla Casella azzurra.

METODO 16 - Una Zona ha 4 Caselle con la stessa Quaterna di Candidati, ma altri Candidati li nascondono (hidden quads).

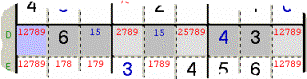Esempio 16: nella Riga D ci sono quattro Caselle (grigio chiaro e azzurra) con la Quaterna 2789 nascosta però in alcune delle quattro. Occorre ripulirle, cominciando ad esempio da quella azzurra da cui va tolto il Candidato 1, ecc.

METODO 17 – Se nessuno dei Metodi precedenti è utilizzabile si deve procedere per Tentativi (Try and error): cioè ipotizzare che un Candidato sia “vero” e vedere le conseguenze della sua propagazione.

Due considerazioni:

- giocare “tentando” con carta e matita (e gomma) può risultare macchinoso;

- giocare “tentando” non è un barare, ma richiede organizzazione e intelligenza.

Il programma SUDOKUPT offre due modalità: (1) tentare considerando “Tutti i Candidati” rimasti o (2) solo quelli che corrispondono a “Doppiette”. In entrambi i casi il programma aggiunge sotto a ciascun Candidato lo spazio in cui compariranno con “v” (vero) o “f” (falso) gli effetti di una prova, senza disturbare la soluzione parziale già raggiunta. Per ulteriori informazioni scaricare il programma SUDOKUPT e leggere il file d’aiuto che l’accompagna.

COME USARE IL PERSONAL TRAINER

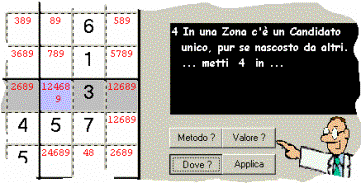Se non si individua una Mossa utile per proseguire il gioco o per accelerarlo, si può ricorrere al Personal Trainer (o Istruttore). Il Personal Trainer dà i suoi Consigli secondo la Priorità standard, 1-17 o modificata dal giocatore.

Per chi vuole imparare esiste una Gradualità di Consigli:

- pulsante “Metodo”: suggerisce sulla Lavagna la tecnica più opportuna in quel preciso momento (nell’es. “4 In una Zona c’è un Candidato unico, pur se nascosto da altri”) e questa informazione può essere sufficiente per riprendere autonomia;

- pulsante “Valore“ (se il “Metodo” non basta): aggiunge sulla Lavagna un’altra riga che dice che cosa si dovrà scrivere o cancellare (nell’es. “… metti 4 in …”); pur non dicendo in quale Casella, l’indicazione può far accendere la scintilla per la Mossa giusta, magari aiutandosi con qualche opportuna Visualizzazione;

- pulsante “Dove” (se si è ancora al buio): colora sullo Schema la Casella da giocare (fondo azzurro) con le Zone in cui si è applicato il Metodo suggerito (fondo grigio) ed eventuali altre Caselle da focalizzare;

- pulsante “Applica” (per i più pigri): per far scrivere la Mossa al programma.

Chi desidera davvero imparare, si farà consigliare provando i primi tre pulsanti nell’ordine suddetto.

I RETICOLI

Il Reticolo di un Candidato è il disegno ottenibile congiungendo con linee orizzontali e verticali le Caselle che in quel momento mostrano la Presenza dello stesso Candidato. Ragionare sulla forma dei Reticoli può aiutare a giocare qualche Mossa corretta. Il programma SUDOKUPT offre anche questa visualizzazione. Ecco quindi alcune forme di Reticoli: si tratta di esempi reali, generati dal programma. Normalmente i Candidati appaiono tutti con un cerchietto vuoto, se però è attiva la scelta “Soluzione” i Candidati veri appaiono con un cerchietto pieno. Negli esempi che seguono tale scelta è attivata e i Candidati veri appaiono con un cerchietto pieno, ma pieno/vuoto dipende dal gioco che era in corso: fare perciò attenzione alle X rosse e ai commenti dei vari esempi.

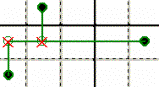
RAMI LIBERI - Sono certamente vere le “cime” e falsi i “nodi”.

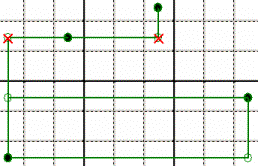
RAMI CON NODI - Partendo dalle “cime” (che come detto sopra sono vere) si deve considerare falso un “nodo” sì e uno no.

RETTANGOLO SEMPLICE - E’ vera l’una o l’altra coppia di vertici opposti: dipende dal caso in esame. Il Rettangolo Semplice è la struttura base che può complicarsi diventando a volte l’X-WING spiegato qui di seguito.

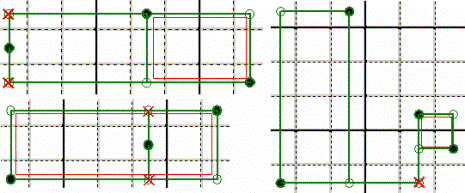X-WING - Se due Righe (o Colonne) hanno solo due Candidati ciascuna e individuano un Rettangolo, allora sono certamente falsi tutti i Candidati presenti al di fuori dei suoi vertici.

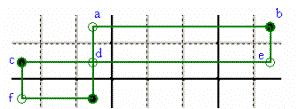
RETTANGOLI INTRECCIATI - E’ vera una delle tre combinazioni: aef, bcg, bdf. Quando il Candidato d manca, sono valide solo le combinazioni aef, bcg. E’ la struttura base su cui si può attaccare lo SWORDFISH spiegato qui di seguito.

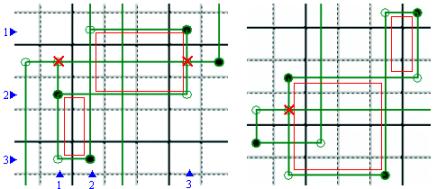SWORDFISH - Se tre Righe (o Colonne) mostrano lo stesso Candidato solo due volte ed esso occupa le stesse tre Colonne (o Righe) in modo da individuare due Rettangoli intrecciati con un vertice in comune, allora sono certamente falsi tutti i Candidati presenti sulle Colonne (o Righe) al di fuori dei vertici. Quanto ai Candidati veri dipende dal gioco.

Nota - Il caso vale anche se sulla Riga (o Colonna) comune c’è il Candidato (totale tre presenze).

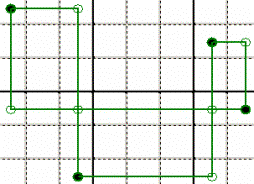PIU’ RETTANGOLI INTRECCIATI (con o senza i Candidati nei vertici in comune) - Qui valgono le varie combinazioni di vertici contrapposti (una è quella mostrata).

RETTANGOLI ANNIDATI - Tre le combinazioni valide possibili (una è qui mostrata).

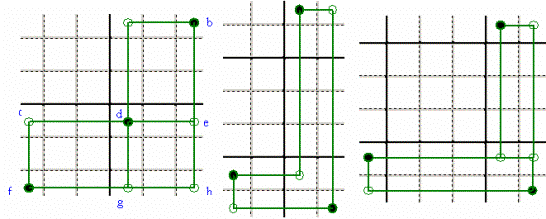
RETTANGOLI A SQUADRA - Nessuna esclusione a priori. Valgono tutte le combinazioni: ach, aef, bdf (qui mostrata), bce. Potrebbe mancare qualcuno dei candidati: d e g h.

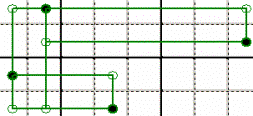SEQUENZA DI SQUADRE - Anche qui valgono altre combinazioni di vertici opposti oltre a quella mostrata.

Buon gioco !

Ritorno al mio Sito