|
Un modello termocinemolecolare per il
dimensionamento dei tubi di De Laval nei razzomodelli |
|
|
Diego
Vecchio alpha.cygni@libero.it |
Premessa termodinamica
I gas che danno propulsione ad un
razzomodello (o ad un razzo vero) hanno origine in una camera di combustione e,
attraverso un ugello detto anche tubo di De Laval, raggiungono l’ambiente
esterno, dove trovano la pressione atmosferica, che indichiamo con 
.
Il tubo di De Laval consiste in un
restringimento progressivo della camera di combustione (detto strozzatura nella
sua sezione minima) che serve a far acquisire velocità ai gas di scarico, e in
un successivo allargamento progressivo che li porta in modo indisturbato fino a
, dal valore di pressione originariamente maggiore nella
camera di combustione.
Senza la strozzatura i gas non
acquisterebbero velocità; senza l’allargamento i gas non si espanderebbero fino
alla pressione atmosferica.
L’aspetto dell’ugello assume dunque
il tipico andamento convergente – divergente, come in fig. 1.
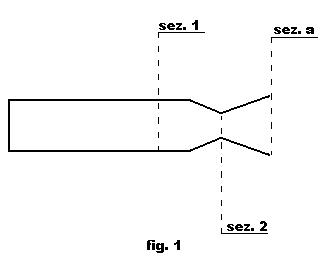
Vi si identificano tre sezioni.
Sez. 1, corrispondente al diametro della camera di combustione; Sez. 2,
corrispondente al diametro della strozzatura; Sez. a, che corrisponde allo
sbocco in atmosfera libera.
Se assumiamo che i gas si
trasformino in modo adiabatico dalla camera di combustione fino all’esterno,
attraversando dunque l’ugello, riscontriamo le seguenti relazioni fra le loro
proprietà nelle Sezioni 1, 2, a, da essi incontrate in successione cronologica:
è il volume
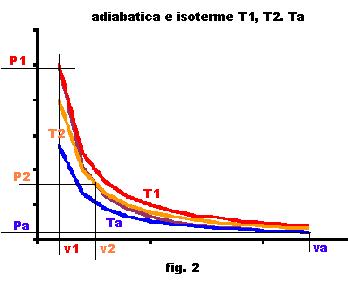
specifico. Questi concetti sono espressi nel grafico di fig. 2, dove la
trasformazione adiabatica è appunto compresa fra le isoterme estreme 
con passaggio
dall’isoterma intermedia 
.
Di questi sei parametri che
descrivono l’espansione dei gas, siano noti quelli di Sez. 1 e 
che è la pressione
atmosferica.
L’essere la trasformazione
adiabatica permette poi di scrivere:
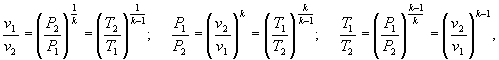
relazioni che valgono anche
ponendovi l’indice 
in sostituzione del 
è il rapporto dei
calori specifici a pressione costante e volume costante, e dunque è un numero
puro.
Dimensionalmente, poiché facciamo
uso del Sistema MKSA, valutiamo le pressioni come
, le temperature 
e i volumi specifici 
.
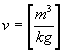Il volume specifico di un gas è il
reciproco della sua densità 
; dunque 
.
Il tubo di De Laval è dimensionato
ottimalmente se, nella strozzatura (Sezione 2), la velocità dei gas è uguale
alla velocità del suono in essi, che vale:
con 
, ed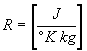 
la costante dei gas,
con le dimensioni qui esplicitate.
il modello termocinemolecolare
Questo
modello considera il gas come un insieme di parti elementari descritte dai seguenti attributi: volume specifico,
temperatura, pressione e velocità, variabili nel corso della trasformazione
dalla camera di combustione all’uscita.
Calcola
dunque le espressioni di questi attributi in funzione dei punti significativi
del tubo di De Laval (ingresso, strozzatura, sbocco in ambiente 
), nel rispetto dei vincoli geometrici delle sue dimensioni,
e ricava la distribuzione delle pressioni al suo interno da cui, per
integrazione sulla superficie, la forza di spinta che complessivamente dà
propulsione al razzo.
La
parte elementare di gas, ancora non meglio specificata, è chiamata, da questo
momento, equimolecola (EQM), ed è descritta dal vettore di
quattro termini, funzione dell’ascissa 
del tubo di De Laval:
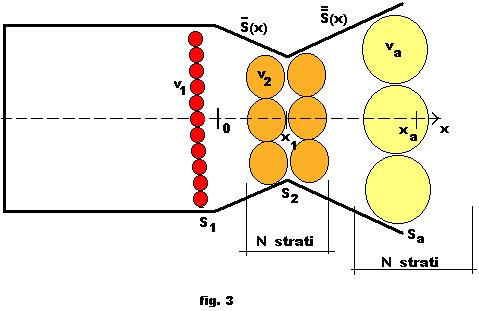
In
fig. 3 le EQM sono rappresentate come
sfere, e ciascuna ha il volume specifico 
funzione dell’ascissa
in cui si trova, alla
quale corrisponde anche la sezione 
.
Le
EQM si espandono e si raffreddano, mentre procedono verso l’uscita del tubo di
De Laval.
E’
dunque giocoforza che, nel tratto convergente, uno strato inizialmente
complanare cominci a disporsi su più strati nel corso del suo procedere, e si
trovi disposto sul numero massimo di 
strati nella sezione 
della strozzatura.
Invece
nella sezione divergente il numero 
di strati può essere
mantenuto invariato, perché pensiamo di allargare il tubo di De Laval in
proporzione all’aumento di volume specifico delle EQM (è quello che intendiamo
per espansione indisturbata).
Si
possono introdurre le seguenti grandezze:
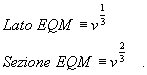
Si
ha allora:
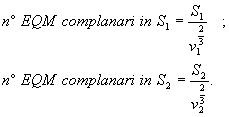
Il
numero degli strati 
in 
, che per il modello sono tutti paralleli fra di loro, è
allora:
.
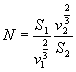La
lunghezza 
transita per 
nello stesso
intervallo di tempo 
in cui 
transita per 
, per cui si può scrivere:
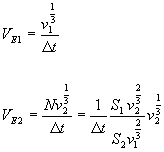
e
dividendo m.a m. si ottiene infine:
che
è la ben nota equazione di contimuità per fluidi comprimibili (cioè a volume
specifico variabile).
In
essa supponiamo noto 
(che faremo
discendere dalla conoscenza del propellente caricato e dalla sua combustione),
il rapporto delle superfici 
(che fisseremo con
criteri di sicurezza, in quanto la strozzatura non deve eccedere certi valori
limite), ed anche 
(che è la velocità di transito delle EQM nella camera di
combustione, e faremo discendere dalla conoscenza del rateo di combustione del
propellente, espresso ad esempio in 
).
Tanto
basterebbe per disegnare la parte convergente del tubo di De Laval; ma per
progettare anche la parte divergente (che influenza del resto il corretto
funzionamento di ciò che sta a monte) necessita la conoscenza di 
e 
, del tutto incognite, che sono il volume specifico e la
temperatura assunte dalla EQM nella strozzatura.
Tuttavia
sappiamo che, nella strozzatura di sezione 
, le EQM devono possedere la velocità del suono; dunque
devono soddisfare alla relazione:
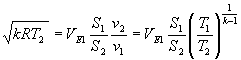
dalla
quale si ricava:
.
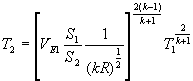Da
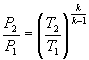e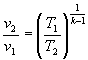 
e dall’equazione di
continuità discendono:
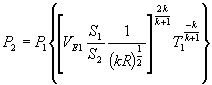[1] ;
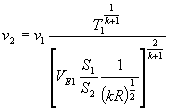[1 bis]
;
.
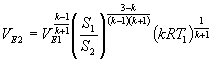Il
vettore 
nella Sezione 2 (strozzatura) è dunque completamente noto
dalle equazioni precedenti:
.
Mettiamoci
adesso nella parte divergente, e precisamente nella Sezione a, dove è nota la 
.
Dall’equazione
dell’adiabatica possiamo scrivere:
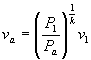[2] .
Poiché
l’espansione è supposta avvenire senza rimescolamento degli strati (tanti
strati in 
quanti in 
), si può istituire una relazione di proporzionalità fra
queste sezioni e quelle delle EQM, per cui:
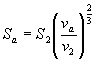[3] ;
La
stessa ipotesi permette di dire che le lunghezze 
e 
transitano nelle
rispettive sezioni nello stesso intervallo di tempo 
, per cui si può scrivere:
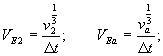dividendo m.a m. si
ottiene:
.
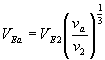La
temperatura dei gas all’uscita è ricavabile sempre da una relazione
dell’adiabatica:
.
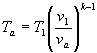In
questo modo è noto il vettore 
.
dal punto di vista progettuale
Riteniamo
noto il vettore 
nella camera di
combustione (nel prossimo paragrafo vedremo come).
Riteniamo
noto 
e, con scelta di
opportunità (come il non eccedere certi rapporti, consolidati come sicuri
dall’esperienza), anche 
. Con la [1] si calcola 
; con la [1 bis] si calcola 
e con la [2] si
calcola 
, necessari per applicare successivamente la
[3]. Infine, con quest’ultima appunto, si calcola 
.
Per
calcolare la spinta esercitata dal motore del razzo, si potrebbe procedere
ricavando il profilo della pressione lungo l’ascissa 
del tubo di De Laval,
ottenendosi la funzione 
, da integrare lungo la superficie.
Per
i razzomodelli è più semplice tuttavia ritenere 
lineare fra due
estremi, che sono 
nel tratto
convergente, e 
in quello divergente.
La
spinta del motore del razzomodello è allora:
, misurata in 
.
chimica-fisica del
propellente
Ipotizziamo
di far uso del propellente composto dalla miscela 
di cui presentiamo nel seguito un’interpretazione delle
reazioni di ossiriduzione:
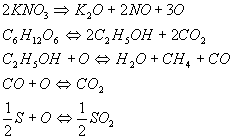
da cui, sommando m.a m., si ottiene:
.
L’equazione
chimica permette di ricavare la composizione ponderale del propellente, a
partire dalle masse molecolari degli elementi chimici che lo costutiscono in
origine (membro di sx dell’equazione), e dal loro coefficiente di Lavoisier
(MML=masse molecolari * coeff. Lavoisier):
Sui
gas di scarico (membro di dx dell’equazione) possiamo calcolare la MML e la
massa molecolare di una “molecola fittizia”, media ponderale delle molecole che
lo compongono:
|
coeff. Lavoisier |
composto |
massa molecolare |
MML |
|
1 |
|
61.982 |
1*61.982=61.982 |
|
2 |
|
30.008 |
2*30.008=60.016 |
|
1 |
|
46.07 |
1*46.07=46.07 |
|
3 |
|
44.011 |
3*44.011=132.033 |
|
1 |
|
18.016 |
1*18.016=18.016 |
|
1 |
|
16.043 |
1*16.043=16.043 |
|
1/2 |
|
64.066 |
(1/2)*64.066=32.033 |
|
|
|
|
Totale=366.193 |
La
massa molecolare della “molecola fittizia” dei gas di scarico è data dunque da:
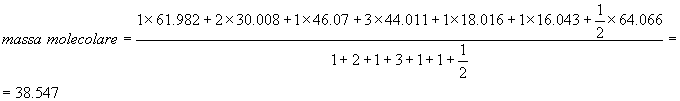
per
cui si può scrivere, per questo propellente:
Procuriamoci
adesso il valore della costante dei gas, 
in unità MKSA,
partendo dalle unità chimiche 
; 
; 
gli ultimi due valori essendo
tipici del propellente ipotizzato.
Si
ottiene 
Le ultime sono
appunto le unità MKSA, e il coefficiente numerico che le esprime varia a
seconda del propellente, perché varia la massa molecolare (dunque 
espressa in unità
MKSA non è una costante universale, mentre lo sarebbe se invece dei 
si facesse uso delle 
).
A
questo punto, conoscendo la densità con cui il propellente è caricato nella
camera di combustione, 
, possiamo calcolare 
con l’equazione di
stato dei gas, sempre in unità MKSA; 
, temperatura di combustione, è da ritenersi nota, così come
la lunghezza 
della camera di
combustione (che del resto è indifferente nel calcolo della
):
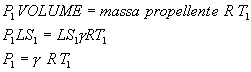
con
le unità di misura MKSA che servono alla bisogna, 
; dunque la pressione
si troverà espressa in 
Alla
conoscenza della EQM nella camera di combustione mancano ancora: 
e 
.
Per
calcolare il primo parametro bisogna conoscere il rateo di combustione del
propellente, 
, nell’ipotesi che, in un dato istante, la combustione
progressiva del propellente espella i gas che si erano già formati. Questo
parametro è un dato sperimentale del propellente.
La
quantità di propellente che deve bruciare è data da 
e ciò avviene nel
tempo:
possiamo immaginare
che ogni molecola di gas, che si origina dalla reazione chimica, debba
percorrere il tratto di camera di combustione fra il fronte di fiamma e
l’imboccatura del tubo di De Laval, che non è costante ma aumenta da 0 a L
durante la combustione stessa.
Poniamo
perciò:
, in unità 
Per
quanto riguarda 
volume specifico
della EQM in 
esso vale
manifestamente 
, in unità 
, perché la massa del propellente incombusto è uguale a
quella dei gas di scarico, ed il volume della camera di combustione è un
invariante.
Con
questo, si hanno tutti gli elementi teorici (non ancora le costanti
sperimentali) per tentare un progetto. Le costanti sperimentali, del resto,
dovrebbero essere note nella letteratura della razzomodellistica, o fatte
discendere da una sperimentazione abbastanza accessibile.
Ancora
un commento sul concetto di equimolecola (EQM): come sarà adesso chiaro, le EQM
sono un volume variabile che è a disposizione di una massa di entità
costante. Così, ad esempio, un kg (o un grammo) di gas è manifestamente una
quantità invariabile nel corso della trasformazione, ma il volume di cui
questa massa può disporre è variabile durante la stessa, perché il gas
si espande mentre percorre il tubo di De Laval. Dunque, a parità di massa, il
volume di cui questa dispone è variabile nel tempo.
Si
è convenuto che questo volume si espanda, mantenendo la forma sferica. Si è
anche fatta l’ipotesi che i volumi sferici delle EQM si tocchino, senza
compenetrarsi.
Federazione Missilistica Europea
