Di Massimo Fantin

HOME

 Premessa di teoria degli insiemi.

Premessa di fisica quantistica

Esempio di accoppiamento con variabile nascosta

Ipotesi della fisica quantistica

Funzionamento del Programma di simulazione

Programma di simulazione

Premessa di teoria degli insiemi.

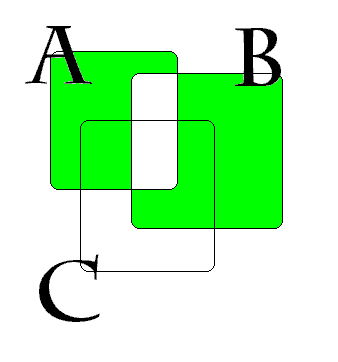
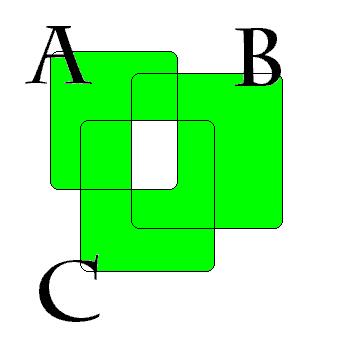
Definiamo differenza simmetrica tra due insiemi A e B l'insieme A ¸ B formato da tutti gli elementi di uno dei due insiemi ma non di entrambi.

Evidentemente la differenza simmetrica gode della proprietà commutativa.

Dati tre insiemi A,B,C ,vale la seguente relazione di contenimento:

A¸ B Í (A¸ C) È ( B ¸ C)

Per dimostrare questa relazione è sufficiente tracciare i diagrammi di Venn del primo e del secondo membro e verificare che tutte le zone che costituiscono la differenza simmetrica di A e B fanno parte anche dell'unione scritta a secondo membro.

Se si suppone che le 8 zone in cui viene diviso il diagramma di Venn di A,B,C contengano un certo numero di elementi e indichiamo con N(A¸ B ), N (A¸ C) e N ( B ¸ C) il numero degli elementi contenuti nei rispettivi insiemi la relazione insiemistica si tradurrà nella:

N(A¸ B ) £ N (A¸ C) + N ( B ¸ C), analogamente se il diagramma rappresenta le probabilità del verificarsi di tre eventi A,B,C la disuguaglianza si traduce nella seguente

disuguaglianza di Bell:

P (A ¸ B ) £ P (A ¸ C) + P ( B ¸ C)

nella quale con il simbolo P (A¸ B ) si indica la probabilità che si verifichi uno degli eventi A o B ma non si verifichi l'altro, mentre . P (A ¸ C) esprime la probabilità che si verifichi l'evento A o C ma non entrambi e P ( B ¸ C) la probabilità che si verifichi B o C ma non entrambi.

Come si è visto la disuguaglianza di Bell è stata dimostrata a partire unicamente da considerazioni logiche pertanto la sua validità è vera indipendentemente da altre ipotesi.

Premessa Questa disuguaglianza sarà importante in seguito per dimostrare l'inadeguatezza delle teoria a variabili nascoste per spiegare il comportamento quantistico delle particelle accoppiate.

Riferimenti bibliografici:

Bernard d'Espagnat La teoria dei quanti e la realtà in Le scienze n137 del gennaio 1980

Gian Carlo Ghirardi Un'occhiata alle carte di Dio Il saggiatore Milano 1997

 Premessa di fisica quantistica.

E' sperimentalmente possibile produrre coppie di particelle accoppiate, (non ci interessa di che particelle si tratta, supponiamo si tratti di fotoni ), Per spiegare cosa intendiamo per particelle accoppiate, supponiamo che queste particelle vengono sottoposte entrambe ad uno stesso test, per esempio di polarizzazione; il test consiste nel verificare se i fotoni passeranno oppure no ciascuna attraverso un filtro polarizzatore avente un certo orientamento. Si verifica che se i due filtri polarizzatori hanno lo stesso angolo di orientazione, entrambi i fotoni passeranno o non passeranno il filtro, ma non succederò che uno passerà (supererà il test) mentre l'altro no. Se invece l'orientazione dei due filtri polarizzatori è diversa succederà che se il primo dei fotoni che viene sottoposto al test lo supererà o non lo supererà , il secondo avrà la probabilità di cos²(a -b ) di comportarsi allo stesso modo del primo. (con a -b intendiamo la differenza tra gli angoli di orientazione dei due filtri polarizzatori). E' evidente che questa condizione comprende il caso dei filtri ugualmente orientati infatti cos 0 =1 ovvero i due rilevatori evidenzieranno gli stessi risultati.

Nel caso si tratti invece di particelle antiaccoppiate la probabilità che la seconda particella superi il test se la prima l'ha superato e viceversa è data da sen²(a -b ), il che significa che se i filtri sono in posizione ortogonale le particelle accoppiate supereranno entrambe o non supereranno entrambe il test perché sen(90°)=1 mentre se i filtri sono paralleli quando una particella supera il test l'altra non lo supererà sen(0°)=0.

Dopo questa premessa ci si può chiedere se questa proprietà delle particelle accoppiate ( per quelle antiaccoppiate si può fare un discorso analogo) è dovuta

• Ad una proprietà di entrambe le particelle che si forma al momento della loro nascita e che permetterà loro di sapere se superare il test oppure no ( ipotesi delle variabili nascoste) oppure
• A una comunicazione dell'esito del test tra la prima particella invia alla seconda permettendo così a quest'ultima e di agire di conseguenza nel modo indicato.

Sembrerebbe più plausibile la prima ipotesi, infatti nel caso di particelle accoppiate si potrebbe pensare che le particelle quando vengono generate possiedano entrambe un certo angolo di polarizzazione e che il test venga superato se l'angolo di orientazione delle particella e quello del filtro di polarizzazione sono in una certa relazione.

Ammettere la seconda ipotesi, sempre nel caso di particelle accoppiate, significa supporre che le particella, al momento del rilevamento si orienti secondo la direzione del filtro polarizzatore se supera il test e in direzione ortogonale se non lo supera e contemporaneamente( per una qualche comunicazione misteriosa ) anche la particella accoppiata si orienti dello stesso angolo, infine, questa seconda particella supererà il test a seconda dell'angolo tra il suo attuale orientamento e quello del filtro polarizzatore. La cosa è corretta se la probabilità di superare il test è pari al cos² dell'angolo tra il suo proprio orientamento e quello del filtro polarizzatore. Questa seconda ipotesi, prevista dalla fisica quantistica, è difficile da accettare perché il nostro ragionamento segue l'ipotesi di località e non ammette la possibilità di comunicazione superluminare tra le particelle.

Non è possibile però accettare la prima ipotesi perché il risultato sperimentale lo contraddice infatti non è possibile trovare alcun sistema a variabili nascoste dal quale si possano prevedere le probabilità della concordanza degli esiti del test compatibili con le frequenza che emergono dai risultati sperimentali.

Prima di fornire la dimostrazione di questo fatto studiamo il miglior caso di accoppiamento di particelle a variabili nascoste ( caso presentato nel programma di simulazione). Supponiamo che al momento della creazione delle particelle accoppiate vengano munite di un stesso angolo g , angolo che costituisce la variabile nascosta. Ciascuna particella supererà il test di polarizzazione nei confronti del filtro di angolo di polarizzazione a se | g - a | < 45° e non lo supererà se 45°< | g - a |<90° , dove naturalmente si intende che se | g - a | >90° si considera il supplementare.
Con queste ipotesi possiamo calcolare le probabilità che, noti gli angoli di polarizzazione dei due filtri a e b le due particelle supero i test con lo stesso risultato. Tale probabilità, è P(a , b )= 1- 2|a -b | / p .
Per calcolare tale probabilità applichiamo la definizione classica di probabilità come rapporto tra i casi favorevoli e i casi possibili. I casi possibili sono gli angoli tra 0 e 90° ovvero p /2. Mentre i casi favorevoli corrispondono all'angolo dato da p /2-| a -b | ( dove per | a - b | si intende il suo supplementare nel caso in cui sia maggiore dell'angolo retto), perché se a = b gli angoli di concordanza vanno da a- p /4 a a+ p /4, in tutto p /2, se invece i due angoli sono diversi, supposto a< b vanno da b - p /4 ad a + p /4 e quindi p /2-| a -b |. Pertanto P(a ,b ) = (p /2-| a -b |)/(p /2);
P(a , b ) = 1- 2|a -b | / p . 

Analogamente nel caso di particelle antiaccoppiate si avrà:

Verifichiamo che in questi casi è verificata la disuguaglianza di Bell citata inizialmente infatti:

P(a , b ) = 2|a -b | / p =  2|a - d + d -b | / p £ 2(|a -d |+|d -b |)= 2|a -d |+2|d -b |=P(a ,d )+P(b ,d ). Che si tratta di una disuguaglianza triangolare.

La seconda ipotesi considerata precedentemente invece concorda con i fatti sperimentali, però non può essere dovuta a variabili nascoste infatti le frequenze verificate sperimentalmente non sono compatibili con le probabilità previste dalla disuguaglianza di Bell. Dimostriamo che se la probabilità di concordanza è quella prevista P(A,B) = cos²(a ,b ) neghiamo la disuguaglianza di Bell.

Supponiamo di disporre di tre filtri polarizzatori A,B,C orientati rispettivamente secondo gli angoli a =0°, b = 15° e g =45°

Calcoliamo le probabilità di concordanza
P(A,B) = cos² ( a - b ) = cos²( 15°) =1/2+Ö3 /4

P(B,C) = cos² ( b - g ) = cos²(30°) = 1/4

P(A,C) = cos²( a - g ) = cos²(45°) = 1/2

Da cui P(A,B) = 1/2 + Ö3 /4 > 1/2 +1/4 = P(B,C) + P(A,C) contro la disuguaglianza di Bell che è stata dimostrata mediante considerazioni generali di logica e teoria degli insiemi e quindi ha una validità superiore alle questioni fisiche a cui si riferiscono le teorie. Questo teorema dimostra l'impossibilità non di una teoria particolare , come quella che ho ipotizzato, ma va bel oltre , nega infatti l'esistenza di ogni possibile teoria a variabili nascoste che prevedono che le particelle accoppiate possiedano una qualche proprietà che permette loro di superare o no i test. In un certo senso pensare che sia possibile che un comportamento a variabili nascoste produca gli effetti sperimentali della fisica quantistica è come pensare che esista un triangolo nel quale un lato sia maggiore della somma degli altri due.

 Per comprendere meglio questi fatti che, risultano piuttosto oscuri ha costruito il programma che permette di simulare il comportamento delle particelle accoppiate, (antiaccoppiate) e esaminare sia il caso previsto dalla meccanica quantistica sia dall'ipotesi delle variabili nascoste. I risultati possono apparire in un primo momento simili ma se si analizza meglio la questione ci si accorge della differenza.

Appare al centro la sorgente di particelle accoppiate (o antiaccoppiate, la scelta si fa con la finestrella in basso). Ai lati appaiono i due filtri polarizzatori spostabili con il mouse agendo al centro di essi, per modificare invece gli angoli di polarizzazione si trascina con il mouse il piano di polarizzazione, gli angoli appaiono scritti sopra al filtro assieme alla differenza tra i due. Sopra e sotto ai filtri ci sono due lampadine che si accendono di verde o di rossa a seconda se il test è stato superato oppure no. Per generare una coppia di particelle si aziona il tasto via. È possibile generare una particella singola oppure 10 o 100 o 1000 particelle in successione. Per accelerare il fenomeno si può agire su v+ mentre v- rallenta. In alto viene prodotta una tabella riassuntiva dei risultati ottenuti con gli stessi angoli ( quando si cambia uno degli angoli si azzerano). La tabella mette a confronto gli esiti dei test delle due particelle. Il grafico in alto a sinistra (nel quale sull'asse orizzontale compaiono gli angoli tra i filtri mentre in quello verticale la probabilità di concordanza delle risposte) visualizza i diversi comportamenti della teoria a variabili nascoste della meccanica quantistica. La prima è rappresentata dalle due diagonali mentre la seconda dalle curve cosinusoidali. Un puntino rosso si posiziona a seconda delle frequenze indicate nella tabella, se il numero delle prove è sufficientemente grande la differenza tra probabilità e frequenza diventa insignificante e il puntino rosso si colloca proprio sulla curva corrispondente a seconda del tipo di esperimento che si sta effettuando.