| home page | | | percorso filosofia |
| | percorso storia |
| | percorso didattica |
| | percorso italiano |
| | percorso semiserio |
| | oltre il sito |
|
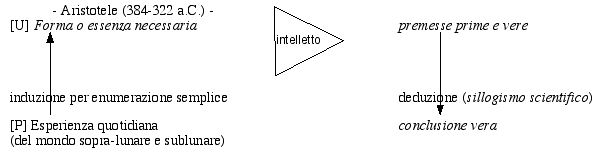 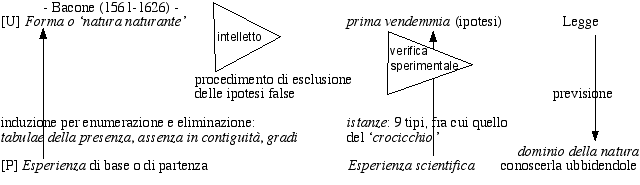 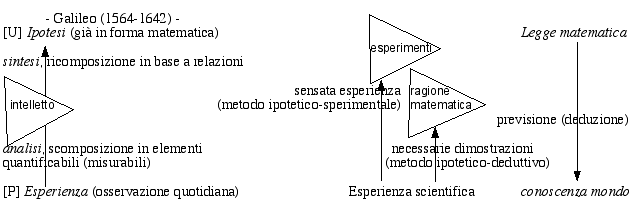 |
- Legenda - I triangoli negli schemi rappresentano momenti di verifica o di scelta con una definizione più precisa o più alta delle conoscenze rispetto a quelle di partenza: ogni triangolo può avere una o più entrate, ma una sola uscita.Il corsivo è usato per i termini specifici dei vari autori. [U] = universale, proposizioni universali; [P] = particolare, proposizioni particolari. |
|
La constatazione più interessante derivabile da questi schemi è l’aumento e la diversificazione dei «triangoli» passando da un autore all’altro2. Aristotele considera l’intelletto come una virtù dianoetica in grado di individuare i principi primi di tutte le scienze (conoscenza vera, episteme), principi che, come tali, non sono ipotesi. Bacone arriva alla ‘prima vendemmia’ come conclusione ipotetica da trarsi dall’analisi delle tavole: evidentemente è una prima conclusione operata dall’intelletto dello scienziato. Galileo, invece, congiunge l’esperienza induttiva con la matematica convinto che il mondo naturale sia scritto in caratteri matematici, le ‘sensate esperienze’ con le ‘necessarie dimostrazioni’, il metodo ipotetico-induttivo (sperimentale) con quello ipotetico-deduttivo (ipotesi matematica con un controllo mediante le conseguenze prevedibili). Dati questi assunti metodologici, è coerente l’uso degli esperimenti mentali5. 1. L’idea degli schemi è ripresa, con varie modifiche e correzioni, da A. Girotti, «La filosofia per unità didattiche», ed. Pagus 1993. 2. «La pluralità di approcci (induttivo, abduttivo, ipotetico-deduttivo) utilizzati per scoprire teorie scientifiche dev’essere considerata una ricchezza da tutelare, anziché una debolezza da evitare, sempre che si tratti di una pluralità di approcci «razionali»» (G. Boniolo e P. Vidali, «Filosofia della scienza», ed. Bruno Mondadori 1999, p. 221). 3. La deduzione (unica forma corretta di ragionamento dimostrativo e di sillogismo, secondo Aristotele) procede dall’universale al particolare, mentre l’induzione vuole procedere dal particolare all’universale (o a una conoscenza di tipo più generale). 4. L’abduzione è anche detta ‘retroduzione’, perché dato un fatto sorprendente si cerca (tornando indietro) una spiegazione ragionevole e convincente per quel fatto. Quindi come l’induzione parte e si basa sempre sul particolare, ma procede indietro e non in avanti. 5. Salviati (Dialogo, a conclusione della I giornata): «[...] pigliando l’intendere intensive... dico che l’intelletto umano ne intende alcune [proposizioni] così perfettamente, e ne ha così assoluta certezza, quanto se n’abbia l’istessa natura; e tali sono le scienze matematiche pure, cioè la geometria e l’aritmetica delle quali l’intelletto divino ne sa bene infinite proposizioni di più, perché le sa tutte, ma di quelle poche intese dall’intelletto umano credo che la cognizione agguagli la divina nella certezza obiettiva, poiché arriva a comprenderne la necessità, sopra la qual non par che possa essere sicurezza maggiore.» Salviati (Dialogo, II giornata): «Io senza esperienza son sicuro che l’effetto seguirà come vi dico, perché così è necessario [...]» Dunque, il metodo ipotetico-sperimentale e la necessità di tipo matematico stanno alla base dell’utilizzo degli esperimenti mentali. |
Mercoledì, 12 novembre 2003