LONG TAILED PAIR STUDIO ANALITICO
Di phase splitter ce ne sono molti tipi, quello sul quale indago in questa pagina è il” Long-Tailed Pair”. Si consideri la figura 1.
 Fig1
Fig1
NOTA: Tutti i parametri dinamici o incrementali li rappresento con lettere minuscole. Quelli statici o in continua li rappresento con le lettere maiuscole.
Il circuito raffigurato in figura serve a generare due segnali sulle uscite vout1 e vout2 tra loro uguali in ampiezza ma sfasati di 180°; il primo è in controfase con vin, mentre il secondo è in fase con vin.
Affinché le due uscite siano identiche in ampiezza occorre che le sue sezioni dello splitter, interessate rispettivamente da U1 e da U2, lavorino con un guadagno tale che le correnti dinamiche in esse circolanti siano identiche in ampiezza ma tra loro in controfase, in modo che nella serie composta da RK’ e da RK” circolerà la solo corrente continua di polarizzazione IK (rispetto IK mentre i1 aumenta i2 diminuisce e quindi IK stessa rimane costante ovvero ik = 0), in questo stato lo splitter si dice essere bilanciato.
Per determinare le condizioni che garantiscano il suddetto bilanciamento occorre indagare sull’amplificatore differenziale generico dal quale deriva il phase splitter di figura1.
In figura 2 ne è rappresentato il circuito reale ed in figura 3 quello equivalente per le solo componenti incrementali.
 Fig2
Fig2
 Fig3
Fig3
Essendo le valvole uguali si suppone abbiano lo stesso fattore di amplificazione u e la stessa resistenza interna rp.
Applico la legge di Kirchhoff in entrambe le maglie del circuito e ottengo le seguenti relazioni:
![]() [1]
[1]
![]() [2]
[2]
Dove u è il fattore di amplificazione. Ma la differenza di potenziale tra la griglia ed il catodo è:
![]() [3]
[3]
![]() [4]
[4]
Sostituendo le espressioni [3] e [4] rispettivamente nelle [1] e [2] si ottiene:
![]() [5]
[5]
![]() [6]
[6]
Che può essere re arrangiata così:
![]() [7]
[7]
![]() [8]
[8]
Le soluzioni per questa coppia di equazioni sono le seguenti:
 [9]
[9]
 [10]
[10]
Nel caso dello splitter di figura 1 sul quale si vuole indagare, una delle due tensioni (vin2) è pari a zero e nella [9] e nella [10] l’eguaglianza tra le due correnti non è rispettata ed
il sistema risulta sbilanciato, infatti se si pone vin2 = 0 le due espressioni diventano:
 [11]
[11]
 [12]
[12]
Ovvero le correnti non risultano essere uguali.
Tornando ora alla [9] e alla [10], si nota che per:
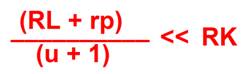 [13]
[13]
Le correnti risultano essere:
 [14]
[14]
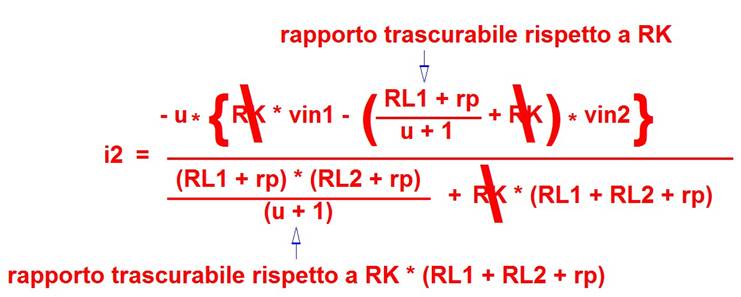 [15]
[15]
Moltiplicando per RL1 ed RL2 per le rispettive correnti e cambiando il loro segno (le valvole invertono il segnale) si ottengono le due tensioni in uscita.
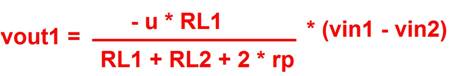 [16]
[16]
 [17]
[17]
Ma per RL1 = RL2 = RL allora:
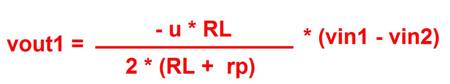 [18]
[18]
 [19]
[19]
Tornando allo splitter di figura1 dove vin2 è pari a 0 le due espressioni si trasformano in:
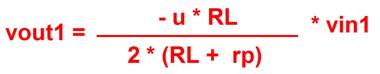 [20]
[20]
 [21]
[21]
Finalmente “javemofatta” J!
Dalle due relazioni si comprende che i due segnali in uscita sono tra loro sfasati di 180° e hanno la stessa ampiezza, per ottenere questo risultato si deve imporre la [13].
Ovviamente per RK tendente all’infinito il circuito tende al perfetto bilanciamento. Ma cosa significa RK molto maggiore di quel rapporto? Ovvero quanto deve essere più grande RK di quel rapporto?
Diciamo che 10 volte superiore da buoni risultati. Purtroppo valori molto alti di RK non sono sempre possibili perché richiederebbero una tensione di alimentazione a sua volta troppo alta, tutto dipende dove deve lavorare lo splitter; in questo caso al posto di una resistenza si può usare un pozzo di corrente attivo. Esso presenta una certa resistenza alla continua ma una molto più alta per la componente incrementale.
Tornando al nostro circuito si nota che le formule [20] e [21] esprimono il guadagno di uno stadio a catodo comune o base comune diviso due; in effetti la tensione incrementale vk dovuta alle correnti i1 e i2 presente ai capi della resistenza RK è di valore molto piccolo (in teoria per un bilanciamento perfetto essa sarebbe pari a zero), è come se i due catodi siano direttamente collegati a gnd tramite una massa virtuale.
Su questa resistenza sarà solo presente la metà della tensione d’ingresso dato che questa alimenta solo una griglia e quindi non viene bilanciata. Da ciò deriva che il guadagno di U1 è quello di un catodo comune alimentato dalla griglia (vgk = vin1 – vk = vin1 / 2), mentre quello di U2 è di una base comune (C mette a massa la griglia) alimentato dal catodo (vgk = 0 - vin1 / 2 = - vin1 / 2).

Fig 4
Il circuito equivalente è rappresentato in figura 5.

Fig 5
Ciao J
Fabio