Logica Matematica

Introduzione al calcolo degli enunciati

1 - Enunciati e connettivi logici

La logica è la scienza della dimostrazione; il fatto che un enunciato sia corretto dal punto di vista grammaticale o semantico non è sufficiente ad assegnare all'enunciato un valore di verità.

Un enunciato è una configurazione linguistica che può essere vera o falsa e non entrambi contemporaneamente.

Un enunciato si compone di enunciati semplici, detti anche parole, indicati schematicamente dalle lettere:

p, q, r, s, …

collegati tra loro da connettivi logici; quelli di impiego più comune sono i seguenti:

È Ç - Þ Û

Il significato dei connettivi logici è il seguente, ed il loro effetto è quello di indurre un determinato valore di verità su di un enunciato composto da enunciati semplici, in funzione del valore di verità di questi ultimi.

Come vedremo, gli ultimi tre possono essere dedotti dai primi due mediante appropriate definizioni.

Nel calcolo si fa uso anche delle parentesi ( ) aventi funzione di delimitazione logica.

È

prende il nome di alternativa o disgiunzione; il valore di verità, da esso indotto sull'enunciato composto p È q, in funzione del valore di verità degli enunciati semplici è il seguente:

p È q è vera quando è vera p "oppure" q (cioè o p o q).

-

prende il nome di negazione; il valore di verità, da esso indotto sull'enunciato composto - p, in funzione del valore di verità dell'enunciato semplice è il seguente:

- p è vera solo se p è falsa (e viceversa).

Ç

prende il nome di congiunzione; il valore di verità, da esso indotto sull'enunciato composto p Ç q, in funzione del valore di verità degli enunciati semplici è il seguente:

p Ç q è vera solo se sono vere p "e" q (cioè sia p sia q).

si ha, per definizione:

p Ç q º - ((- p) È (- q))

Þ

prende il nome di implicazione o condizionale; il valore di verità, da esso indotto sull'enunciato composto p Þ q, in funzione del valore di verità degli enunciati semplici è il seguente:

p Þ q è falsa solo se p è vera e q è falsa (è vera negli altri casi).

si ha, per definizione:

p Þ q º (- p) È q

se p è una condizione, si usa dire:

p è condizione sufficiente per q

se q è una condizione, si usa dire:

q è condizione necessaria per p

Û

prende il nome di coimplicazione o bicondizionale; il valore di verità, da esso indotto sull'enunciato composto p Þ q, in funzione del valore di verità degli enunciati semplici è il seguente:

p Û q è vera solo se p e q sono entrambi veri o entrambi falsi.

si ha, per definizione:

p Û q º ( p Þ q ) Ç ( q Þ p )

se p è una condizione, si usa dire:

p è condizione necessaria e sufficiente per q

Il simbolo Û istituisce una equivalenza logica tra gli enunciati p e q.

2 - Funzioni e tavole di verità

Un connettivo logico costituisce una funzione di verità, nel senso che associa a ciascun valore di verità degli enunciati semplici componenti un dato valore di verità dell'enunciato composto.

Per meglio comprendere il funzionamento dei connettivi logici è molto utile fare ricorso al metodo delle tavole di verità.

Si riporta, di seguito la tavola di verità degli enunciati composti già presentati; il valore di verità "vero" è contrassegnato con la lettera "V", il valore di verità "falso" è contrassegnato con la lettera "F".

p

q

p È q

- p

p Ç q

p Þ q

p Û q

V

V

V

F

V

V

V

V

F

V

F

F

F

F

F

V

V

V

F

V

F

F

F

F

V

F

V

V

Se consideriamo l'enunciato (vedi definizione di congiunzione):

- ( p Ç q ) Û - p È - q (*)

si ha:

p

q

p Ç q

- ( p Ç q )

- p

- q

- p È - q

- ( p Ç q ) Û - p È - q

V

V

V

F

F

F

F

V

V

F

F

V

F

V

V

V

F

V

F

V

V

F

V

V

F

F

F

V

V

V

V

V

Ed in tal caso l'enunciato dato è vero qualunque siano i valori di verità degli enunciati semplici.

E' facile verificare che anche l'espressione seguente:

- ( p Ç q ) Þ - p È - q (**)

assume il valore di verità vero, a prescindere dai valori di verità degli enunciati semplici.

3 - Tautologie e contraddizioni

Se una forma enunciativa assume sempre il valore di verità "vero" indipendentemente dai valori di verità degli enunciati semplici essa si dice espressione valida o tautologia o identità.

Si suole dire che tali espressioni universalmente vere sono semanticamente invarianti.

Si chiama operazione di falsificazione, quella di anteporre il connettivo logico - (negazione) ad una espressione universalmente vera in modo che essa diventi universalmente falsa; l'espressione universalmente falsa si dice contraddizione.

Esempio: nel caso dell'implicazione (**) si ha che - ( p Ç q ) implica logicamente - p È - q o anche che - p È - q è una conseguenza logica di - ( p Ç q ).

Esempio: nel caso della coimplicazione (*) si ha che - ( p Ç q ) e - p È - q sono logicamente equivalenti.

Sussistono per le tautologie i seguenti teoremi.

Teorema 1

Se p e p Þ q sono due tautologie, allora anche q è una tautologia.

Dimostrazione: p Þ q può essere falsa solo se q è falsa, oppure p Þ q può essere vera e p e q possono essere entrambe false, ma p Þ q è una tautologia ed inoltre anche p è sempre vera, quindi q non può essere falsa ed è vera sempre e quindi q è pure una tautologia.

Teorema 2

Se p è una tautologia e la forma enunciativa q si ottiene da p sostituendo forme enunciative di q a forme enunciative di p, allora anche q è una tautologia.

Esempio: se - ( p Ç q ) Û - p È - q è una tautologia, anche - ( p Ç r ) Û - p È - r è una tautologia ottenuta dalla prima sostituendo alla forma enunciativa q la forma enunciativa r.

Dimostrazione: p è una tautologia a prescindere dai valori di verità degli enunciati semplici componenti, quindi la sostituzione di questi non apporta variazioni al valore di verità della forma enunciativa composta.

4 - Il calcolo degli enunciati E.

Abbiamo visto come, ricorrendo alle tavole di verità, si possibile assegnare valori di verità alle forme enunciative composte.

Tuttavia per lo sviluppo completo e più approfondito degli aspetti logici, occorre ricorrere ad un metodo, altamente efficace, il metodo assiomatico; ne sarà data di seguito concreta applicazione presentando una teoria formale assiomatica.

Una teoria formale assiomatica T resta definita se si verificano le seguenti condizioni:

  1. esiste un insieme finito di simboli di T;

  2. esiste un insieme di sequenze finite di simboli che prendono il nome di formule;

  3. esiste un sottoinsieme dell'insieme delle formule di T, detto insieme delle formule ben formate (f.b.f.);

  4. esiste un sottoinsieme di f.b.f. privilegiate, a cui si dà il nome di assiomi;

  5. esiste un insieme finito di relazioni tra f.b.f. di T, dette regole di inferenza; se R è una tale regola e se una f.b.f. p è nella relazione R con n f.b.f., allora si dice che p consegue direttamente dalle n f.b.f. mediante la R.

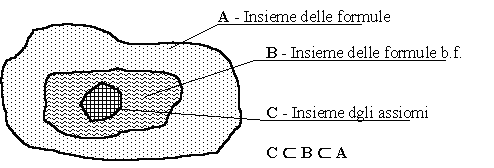
Si hanno le seguenti definizioni

Definizione 1

Si dice dimostrazione in T un insieme finito di f.b.f. p1, p2, p3, …, pn tali che ognuna di esse o è un assioma o consegue direttamente da quelle che la precedono mediante una delle regole di inferenza.

Definizione 2

Una f.b.f. di T che sia l'ultima di una dimostrazione, si dice Teorema.

Definizione 3

Una teoria T si dice decidibile se esiste un metodo meccanico (algoritmo) per stabilire se, data una qualsiasi f.b.f. p di T, esiste una distrazione di p; nel caso contrario T si dice indecidibile.

Definizione 4

Dato nella teoria T un insieme F di f.b.f., se esiste una sequenza p1, p2, p3, …, pn di f.b.f tali che ognuna o è un assioma, o è una f.b.f. di F o consegue direttamente da f.b.f. precedenti nella sequenza e che p = pn, allora si dice che la f.b.f. p e una conseguenza di F in T.

Nel caso di tale ultima definizione, la sequenza di f.b.f. di dirà dimostrazione o deduzione di p da F, mentre gli elementi di F si diranno ipotesi della deduzione, e si suole usare il simbolo:

F ¬ p

per indicare che p è una conseguenza di F.

Poiché F è un insieme di f.b.f. , { p1, p2, p3, …, pn } tale simbolo diventa:

{ p1, p2, p3, …, pn } ¬ p

e se tale insieme è vuoto il simbolo diventa: ¬ p e ciò vuol dire che p è un teorema di T (Definizione 2).

Una definizione più rigorosa è la seguente.

Definizione 5

Dato un insieme F di f.b.f. , { p1, p2, p3, …, pn }, si dice che la f.b.f. p è deducibile dalle f.b.f. { p1, p2, p3, …, pn }, se:

  1. per una qualsiasi f.b.f. pk di F si ha: { p1, p2, p3, …, pn } ¬ pk

  2. per una qualsiasi f.b.f. p di T si ha: { p1, p2, p3, …, pn } ¬ p

  3. se per le f.b.f. p e p Þ q si ha { p1, p2, p3, …, pn } ¬ p e { p1, p2, p3, …, pn } ¬ ( p Þ q ) allora si ha { p1, p2, p3, …, pn } ¬ q

 

5 - Il linguaggio di E.

Procediamo ad illustrare una teoria formale assiomatica del calcolo degli enunciati E.

  1. I simboli di E sono:

    2. È Ç - Þ Û ( )

    e le lettere enunciative p1, p2, p3, …, pn aventi ad indice numeri naturali;

  2. tutte le lettere enunciative p1, p2, p3, …, pn e tutti i simboli sono formule, come sono formule tutte le sequenze finite di tali simboli;

  3. si definiscono cinque operazioni fondamentali tra formule, e cioè:

    4. p È q - p p Ç q p Þ q p Û q

  4. si definiscono rigorosamente le f.b.f. di E nel modo seguente:

  1. tutte le lettere enunciative sono f.b.f.;

  2. se p e q sono f.b.f., tali sono anche p È q, - p, p Ç q, p Þ q, p Û q;

  3. sono f.b.f. solo quelle formule determinate come descritto in a) e b); in altre parole sono f.b.f. tutte e sole le lettere enunciative e quelle che a partire da tali lettere, si costruiscono combinandole per mezzo dei connettivi logoci introdotti;

  1. siano p e q f.b.f. di E; sono assiomi di E le seguenti f.b.f.:

    2. A1) ( p Þ ( q Þ p ))

    A2) ( p Þ ( p Þ r )) Þ (( p Þ q ) Þ ( p Þ r ))

    A3) ( - q Þ - p ) Þ (( - q Þ p ) Þ q )

    A4) p Ç q Þ p

    A5) p Ç q Þ q

    A6) ( p Þ q ) Þ (( p Þ r ) Þ ( p Þ ( q Ç r )))

    A7) p Þ p È q

    A8) q Þ p È q

    A9) ( p Þ r ) Þ (( q Þ r ) Þ (( p È r ) Þ r ))

    A10) ( p Þ q ) Þ (( - p Þ - q ) Þ (( p È q ) Þ r ))

    A11) p Þ - - p

    A12) - - p Þ p

  2. le regole di inferenza di E sono:

R1) se p è una f.b.f. di E contenente la lettera enunciativa p1 la formula q ottenuta da p sostituendo ogni occorrenza di p1 nella p con una qualsiasi formula r è ancora una f.b.f. di E; questa regola è detta regola di sostituzione: in simboli RS;

R2) se p e p Þ q sono f.b.f. di E, allora anche q è una f.b.f. di E; questa regola è detta regola del modus ponens: in simboli MP.

Con le regole precedenti si costruita una teoria formale assiomatica E.

E' possibile dimostrare i seguenti teoremi.

Teorema 1

( p Ç q ) Þ ( q Ç p )

Teorema 2

( p Þ q ) Þ ( q Þ p )

Teorema 3

- - - p Þ - p

Teorema 4

p Þ p

Teorema 5 (teorema di deduzione)

Siano F = { p1, p2, p3, …, pn } un insieme di f.b.f., p e q due qualsiasi f.b.f. di E, se { p1, p2, p3, …, pn } ¬ q, allora { p1, p2, p3, …, pn } ¬ ( p Þ q )

Teorema 6

{ ( p Þ q ), ( q Þ r ) } ¬ ( p Þ r )

Questo teorema fornisce un'ulteriore regola di deduzione detta regola del sillogismo che può essere enunciata:

R3) se p Þ q e q Þ r sono f.b.f. di E, allora anche p Þ r è una f.b.f. di E;

Teorema 7

{ ( p Þ ( q Þ r )), q } ¬ ( p Þ r )

Questo teorema fornisce un'ulteriore regola di deduzione detta regola di inversione degli antecedenti, ossia:

R4) se p Þ ( q Þ r ) è una f.b.f. di E, allora anche q Þ ( p Þ r ) è una f.b.f. di E;

Teorema 8

{ p } ¬ q Þ p Ç q

Questo teorema fornisce un'ulteriore regola di deduzione, ossia:

R5) se p e q sono f.b.f. di E, allora anche p Ç q è una f.b.f. di E;

da R5 e dagli assiomi A4 a A5 si ottiene la regola di deduzione:

R6) se p Ç q è una f.b.f. di E, allora anche p e q sono f.b.f. di E;

infine da R5 e R6 si ottiene la regola di deduzione:

R7) se p Ç q è una f.b.f. di E, allora anche q Ç p è una f.b.f. di E;

Teorema 9

{ p Þ ( q Þ r ) } ¬ ( p Ç q ) Þ r

Teorema 10

{ (( p Ç q ) Þ r ) , p, q } ¬ q Þ r

Questo teorema fornisce ulteriori due regole di deduzione, la prima delle quali è detta regola di riunione degli antecedenti:

R8) se p Þ ( q Þ r ) è una f.b.f. di E, allora anche ( p Ç q ) Þ r è una f.b.f. di E;

R9) se ( p Ç q ) Þ r è una f.b.f. di E, allora anche p Þ ( q Þ r ) è una f.b.f. di E.

6 - Coerenza e completezza di E.

La coerenza o consistenza di una teoria formale assiomatica è quella proprietà della teoria T consistente nel fatto che mediante l'uso del calcolo non è possibile dedurre una data espressione ed anche la sua negazione.

Alternativamente si dice che la teoria è incoerente o inconsistente e non ha alcun valore logico.

Se un calcolo è coerente in tale senso, si dice che esso è sintatticamente coerente, nel senso che si prescinde (nella definizione di coerenza) dal significato particolare delle espressioni considerate.

Esempi di coerenza sintattica sono forniti da svariati calcoli logici e matematici; ad esempio il sistema dell'aritmetica costituisce un caso del genere.

Il teorema di Gödel (teorema di incompletezza) ha mostrato che la prova di coerenza di un calcolo logico non può essere trovata con gli strumenti del calcolo stesso, ma necessita di un ricorso a metodi intuititivi che forniscano un modello per tutte le espressioni del calcolo.

E' legittimo chiedersi se la teoria E su introdotta, ossia il calcolo degli enunciati, è o non coerente; la risposta è affermativa ed è data dal seguente:

Teorema

Il calcolo degli enunciati è coerente; ossia, nella teoria E non esiste alcuna f.b.f. p tale che sono teoremi di E sia p sia - p.

La teoria E è stata costruita a partire da un sottoinsieme delle f.b.f. di E, definite come assiomi, e deducendo da queste, mediante le regole di deduzione altre f.b.f.; ci si pone il seguente problema:

Un assioma di quelli introdotti può essere dimostrato a partire dagli altri ?

Se la risposta fosse affermativa, è evidente che tale assioma può essere eliminato dal gruppo degli assiomi per venire dedotto dagli altri, costituendo così un teorema.

Gli assiomi che non possono dedursi dagli altri vengono detti indipendenti ed indipendente viene detto il sistema di assiomi in cui nessuno di essi può messere dedotto dai rimanenti.

Se ciò non accade, il sistema si dice dipendente e contiene assiomi sovrabbondanti e, come tale, è meno perfetto, anche se a volte è conveniente utilizzarlo in quanto facilita la dimostrazione di particolari teoremi della teoria.

Nel caso della teoria E si può dimostrare che il sistema di assiomi introdotto per essa è un sistema indipendente.

Per le ipotesi di base poste, le formule ben formate che si deducono dagli assiomi, e gli assiomi stessi di una teoria T sono tautologie.

Infatti per definizione, gli assiomi sono espressioni supposte vere a prescindere dalle espressioni enunciative componenti e l'insieme di tutte le altre espressioni derivate è una conseguenza delle premesse assunte (assiomi e regole di deduzione).

Per completezza sintattica del calcolo (cioè prescindendo dagli scopi del calcolo: semantica) si intende la seguente proprietà di esso: se si aggiunge all'insieme delle espressioni del calcolo una nuova espressione, per ipotesi non dimostrabile dagli assiomi e dalle regole di deduzione, allora, dopo tale aggiunta il calcolo diventa contraddittorio.

Se indichiamo con Pr l'insieme delle premesse del nostro calcolo, con C(Pr) l'insieme delle espressioni che ne sono conseguenza, con D(Pr) l'insieme delle espressioni derivabili dal calcolo, allora un teorema di completezza si riduce a dimostrare la relazione seguente:

C(Pr) Í D(Pr)

e cioè che l'insieme di tutte le espressioni che sono conseguenza delle premesse assunte è contenuto nell'insieme delle espressioni derivabili dagli assiomi e dalle regole di deduzione.

Pertanto data un'espressione p tale che:

p Ï D(Pr)

non può essere mai conseguenza delle premesse assunte e la sua introduzione introduce una contraddizione nel calcolo; tale proprietà viene anche denominata completezza in senso stretto.

Si dimostra che il calcolo degli enunciati E è completo in senso stretto.

Abbiamo visto che ogni teorema di E è una tautologia; ci si chiede se è vero l'inverso, e cioè se ogni tautologia è un teorema di E.

Quello enunciato, è noto come problema della completezza di E in senso ampio.

In generale tale problema si pone per qualsiasi teoria formale assiomatica in quanto, nel costruire tale teoria, è sempre necessario sapere se le f.b.f. assunte come assiomi e le regole di deduzione introdotte permettono di dimostrare come teoremi tutte quelle f.b.f. che, nella corrispondente interpretazione non formale di quella teoria, sono delle tautologie.

A questo problema dà soluzione il seguente:

Teorema

Ogni f.b.f. di E che sia una tautologia è anche un teorema di E.