Lezione
XXI
frames
noframes
Strutture dati: le liste parte 2, alberi binari
Introduciamo, in questa lezione, alcune varianti della rappresentazione collegata (o concatenata) delle liste .
In particolare, introduciamo la rappresentazione cosiddetta “circolare” e la rappresentazione simmetrica (rappresentazione di una lista doppia).
Nella rappresentazione collegata circolare abbiamo, che l’ultimo elemento invece di contenere un riferimento nullo, contiene un riferimento al primo nodo della lista stessa.
Graficamente la possiamo immaginare come in Fig. 21.1
![]()

Fig. 21.1 Rappresentazione circolare
La rappresentazione simmetrica delle liste, prevede che ogni nodo della lista contenga due riferimenti: il riferimento al nodo successivo ed il riferimento al nodo precedente;
In Fig. 21.2 abbiamo schematizzato una lista doppia contenente (3,1,5)
![]()

Fig. 21.2 Rappresentazione simmetrica
Attraverso la rappresentazione della lista di fig. 21.2 si puo’ scandire la lista in entrambe le direzioni, avanti ed indietro.
![]()
Fig.
21.3
Nodo in una lista simmetrica
Introducendo le seguenti definizioni:
typedef enum{TRUE=1,FALSE=0}booleano;
typedef int Tipo_atomi;
struct Struct_lista{
Tipo_atomi
info;
struct
Struct_lista *next;
struct Struct_lista *back;
};
typedef struct Struct_lista Tipo_nodo_lista;
typedef Tipo_nodo_lista *Tipo_lista
si definisce una lista doppia, attraverso l’uso di struct e puntatori.
Una lista che utilizza due puntatori, presenta due vantaggi rispetto alle liste semplici: 1) la lista puo’ essere letta in tutte e due le direzioni, utile sia nell’ordinamento, sia nella ricerca; 2) se uno dei due puntatori, non e’ valido la lista puo’ essere ricostruita, usando l’altro puntatore.
Uno svantaggio e’ che richiede uno spazio di memoria maggiore per essere memorizzata, causa i riferimenti all’indietro, aggiuntivi rispetto alle liste semplici.
I tre casi che possono verificarsi inserendo un nuovo elemento in una lista doppia sono: inserimento in testa, inserimento centrale, inserimento in coda alla lista.
Vediamo l’inserimento in testa facendo uso di una simbologia grafica maggiormente chiarificatrice, di un nodo di una lista doppia:
Fig. 21.4

Fig. 21.5 Situazione iniziale:
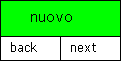
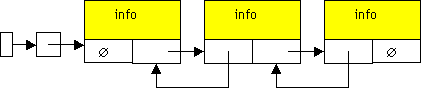
lis *lis
Fig. 21.6 situazione finale: modifichiamo i puntatori per effettuare l’inserimento in testa del nodo avente come campo info, il valore nuovo.
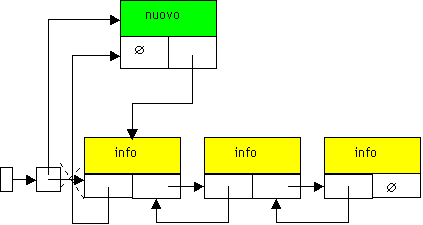
lis *lis
Per gli altri due casi di inserimento di un nodo le operazioni grafiche
da effettuare, sono intuibili dall’esempio su menzionato.
La funzione, per l’inserimento in testa nelle liste doppie, Cons la possiamo cosi’ tradurre in linguaggio C:
Tipo_lista
Cons(Tipo_lista *lis,Tipo_atomi elem)
{
Tipo_lista punt_nuovo;
punt_nuovo=malloc(sizeof(Tipo_nodo_lista));
punt_nuovo->info=elem;
(*lis)->back=punt_nuovo;
punt_nuovo->next=*lis;
punt_nuovo->back=NULL;
*lis=punt_nuovo;
return(*lis);
}
Liste composite
Sono liste i cui elementi possono essere a loro volta delle liste.
Con il tipo di dato astratto risultante si possono definire sia gli alberi che i grafi.
La lista composita (lista) e’ un concetto di lista in generale.
Definizione
Il tipo lista e’ un tipo astratto di dati <S,O,C> con
1) S ={ lista,atomo,booleano}, in cui lista e’ il dominio di interesse;
2) O ={Cons,Car,Cdr,Null,Test_atomo} dove
Cons: (lista U atomo) X listaàlista
Car: listaà(lista U atomo)
Cdr: listaàlista
Null: listaàbooleano
Test_atomo: (lista U atomo)àbooleano
3) C ={lista_vuota}
Nota Car puo’ restituire un valore che appartiene od all’insieme atomo od all’insieme lista.
Test_atomo restituisce TRUE se il suo argomento e’ un atomo, FALSE se e’ una lista.
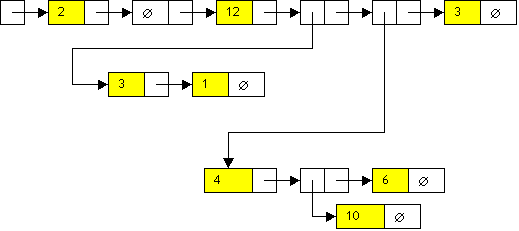
Esempio di lista composita espressa, sia nella sua rappresentazione parentetica, che nella rappresentazione collegata “in forma grafica”.
L=(2 () 12 (3 1) (4 (10) 6) 3)
Fig. 21.7
Alberi
binari
Gli alberi sono un tipo di dato astratto che puo’ essere utilizzato per rappresentare relazioni gerarchiche fra oggetti (in informatica l’albero riveste un ruolo fondamentale).
Un albero A e’ un grafo, in cui esiste un nodo detto radice ed n nodi successori f1,f2,...,fn, della radice con n>=0; tutti i nodi di A tranne la radice, possono essere ripartiti in n insiemi disgiunti A1 … An, aventi a loro volta radice f1,..,fn rispettivamente.
Noi ci occupiamo solo degli alberi binari, i quali sono una struttura di dati astratta, in cui ogni nodo ha al massimo due figli.
Esempio di albero binario: Fig.
21.8
nodo
radice
foglie o nodi terminali
parte della terminologia
relativa agli alberi:
a) livello di un nodo x : e’ la distanza dalla radice al nodo x (distanza intesa come numero di archi che collegano la radice al nodo in questione x)
b) profondita’ o altezza dell’albero: e’ il massimo livello dei nodi di un albero
c) foglie: sono i nodi terminali dell’albero (nodi senza figli)
d) relazione fra i nodi: padre, figlio, fratello…tipo le relazioni parentali.
In un albero A la nozione di “livello di un nodo x” e’ cosi’ definita:
1) la radice ha livello 0
2) se un nodo di A, ha livello k, tutti i suoi figli hanno livello k+1
Si parla di albero ordinato, se si impone una relazione d’ordine fra i figli di ogni nodo.
Un albero con n nodi ha esattamente n-1 archi.
Definizione
a
Un albero binario A e’ un grafo orientato, che o e’ vuoto (non contiene nodi) oppure e’ formato da un nodo R (detto radice) e da due sottoalberi, i quali sono a loro volta alberi binari, (che vengono chiamati sottoalbero sinistro e sottoalbero destro).
Si definisce completo un albero binario, se ogni suo nodo, che non sia una foglia, ha un numero di figli pari a 2 e tutte le foglie appartengono allo stesso livello.
Possiamo dedurre che un albero binario completo avente profondita’ k, ha un numero di foglie pari a: 2^k.
L’albero della figura 21.8 e’ un albero binario ma non e’ completo.
Vediamo adesso, nella Tabella 1, il numero di nodi posseduti da un albero binario completo, per ogni livello k (con k=0,1,...,n)
Tabella 1
|
Livello k |
Numero di nodi |
Nodi per livello |
Tipo nodo rispetto alla
radice |
|
0 |
1 |
2^0 |
Radice o padre |
|
1 |
2 |
2^1 |
figli |
|
2 |
4 |
2^2 |
nipoti |
|
3 |
8 |
2^3 |
pronipoti |
Il numero di nodi totale per livello, di un albero binario completo, avente profondita’ l con l>=0 e’: 2^l.
Il numero totale di nodi di un albero binario completo, avente profondita’ k e’ pari alla somma:
2^0 +2^1+2^2+ …+2^k =2^(k+1)-1
Se k=3 come in tabella1, avremo un numero totale di nodi pari a 2^4 -1 =15
Definizione[1]
L’albero binario e’ un tipo astratto di dati <D,O,C>, con:
a) D ={Alb_bin, Nodo, Booleano}, Alb_bin e’ il dominio di interesse;
b) O ={radice, left, right, costruisci, test_albero_vuoto}, dove:
test_albero_vuoto: Alb_binàBooleano
costruisci: Alb_binXNodoXAlb_binàAlb_bin
radice: Alb_binàNodo
left: Alb_binàAlb_bin
right: Alb_binàAlb_bin
c) C ={albero_vuoto}
test_albero_vuoto e’ una operazione che si applica ad un albero binario e restituisce TRUE se l’albero non contiene nessun nodo, altrimenti FALSE.
costruisci(S,R,D) costruisce un albero binario avente radice R, sottoalbero sinistro S e sottoalbero destro D.
radice applicata ad un albero non vuoto, restituisce il valore associato alla radice dell’albero.
Visite di un
albero binario
Un albero binario si visita, (per visualizzare, elaborare, modificare il contenuto informativo dei suoi nodi) attraverso tre algoritmi principali:
1) visita in preordine
2) visita in postordine
3) visita simmetrica
Consideriamo il seguente albero binario non completo:
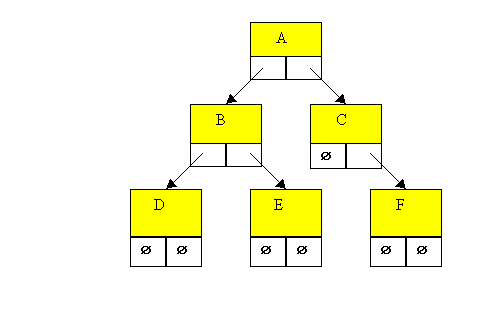
Fig. 21.8
La visita di un albero non vuoto, in preordine o visita in ordine anticipato, richiede l’analisi della radice e poi la visita effettuata con lo stesso metodo del sottoalbero sinistro e del sottoalbero destro.
Un algoritmo ricorsivo che si puo’ formulare per tale visita e’:
visita in preordine l’albero binario A:
if( test_albero_vuoto(A)==FALSE)
{
analizza radice(A);
visita in preordine l’albero binario left(A);
visita in preordine l’albero binario right(A);
}
Applicando la visita in
preordine all’albero binario della Fig. 21.8 avremo che i nodi che si analizzano sono nella
sequenza : A B D E C F.
La visita in postordine ha un algoritmo come il seguente:
visita in postordine l’albero binario A:
if( test_albero_vuoto(A)==FALSE)
{
visita in postordine l’albero binario left(A);
visita in postordine l’albero binario right(A);
analizza radice(A);
}
Nella figura 21.8 avremo utilizzando tale algoritmo la seguente sequenza:
D E B F C A
La visita simmetrica ha un algoritmo come il seguente:
visita in ordine simmetrico l’albero binario A:
if( test_albero_vuoto(A)==FALSE)
{
visita in ordine simmetrico l’albero binario left(A);
analizza radice(A);
visita in ordine simmetrico l’albero binario right(A);
}
Nella figura 21.8 avremo utilizzando tale algoritmo la seguente sequenza:
D B E A C F
Rappresentazione
di un albero binario
Rappresentazione
sequenziale
Il tipo di dato astratto albero binario, puo’ essere rappresentato attraverso il tipo concreto array; ogni valore del tipo albero binario si rappresenta attraverso un valore dell’array monodimensionale.
Le componenti dell’array sono dello stesso tipo dei nodi dell’albero.
Esempio in tabella 2, rappresentiamo l’albero della fig. 21.8 con un array, seguendo le seguenti regole: la radice si memorizza in posizione 0, se un nodo x dell’albero e’ memorizzato in posizione j, il figlio sinistro e’ memorizzato in posizione 2*j+1 mentre il figlio destro e’ memorizzato in posizione 2*j+2 “se esistono”.
Tabella 2
|
indice |
esiste |
info |
|
0 |
TRUE |
A |
|
1 |
TRUE |
B |
|
2 |
TRUE |
C |
|
3 |
TRUE |
D |
|
4 |
TRUE |
E |
|
5 |
FALSE |
H |
|
6 |
TRUE |
F |
Nel linguaggio C possiamo usare le seguenti definizioni per rappresentare l’albero binario:
typedef enum{TRUE=1,FALSE=0}Booleano;
typedef char Tipo_atomi;
#define
MAX_NODI 7;
struct Struct_albero_bin{
Tipo_atomi
info;
Booleano esiste;
};
typedef struct Struct_albero_bin Tipo_nodo_albero;
typedef Tipo_nodo_albero
Tipo_albero_bin[MAX_NODI];
Notiamo come ogni nodo dell’albero binario, in conformita’ alla Tabella 2, sia rappresentato da un array di 7 strutture, in cui ogni struttura e’ costituita da due campi: il campo info ed il campo esiste.
Esercizio
/*Lettura da file di un albero in rappresentazione parentetica, e traduzione in forma di array. Scrittura dell'albero in rappresentazioneparentetica.*/
#include<stdlib.h>#include<assert.h>
typedef enum{TRUE=1,FALSE=0}Booleano;
typedef char Tipo_atomi;
#define MAX_NODI 100;
struct
Struct_albero_bin{
Tipo_atomi info;
Booleano esiste;
};
typedef
struct
Struct_albero_bin Tipo_nodo_albero;
typedef Tipo_nodo_albero
Tipo_albero_bin[MAX_NODI];
/* legge il prossimo carattere diverso da spazio nel file */char LeggiParentesi(FILE *f){ char car;car = getc(f); /* legge il carattere */
if (car == '\n') car = ' ';while(car != '(' && car != ')') { /* se e' =' ' ne legge un altro */
car = getc(f); if (car == '\n') car = ' ';}
return car;} /* LeggiParentesi */
/* legge un sottoalbero */void LeggiSottoAlbero(FILE *file_albero, int j,Tipo_albero_bin albero){ char car; Tipo_atomi i;car = LeggiParentesi(file_albero); /* legge la parentesi aperta */
car = getc(file_albero); /* carattere successivo */
if (car == '\n') car = ' '; if (car== ')') { albero[j].esiste = FALSE;/* se legge () allora l'albero e' vuoto */
return; }fscanf(file_albero, "%c", &i); /* altrimenti legge la radice */
albero[j].esiste = TRUE; albero[j].info = i; /* legge i sottoalberi */ LeggiSottoAlbero(file_albero, j*2 + 1, albero); LeggiSottoAlbero(file_albero, j*2 + 2, albero); car=LeggiParentesi(file_albero); /* legge la parentesi chiusa */
} /* LeggiSottoAlbero */
/* legge un albero */void LeggiAlbero(char *nome_file, Tipo_albero_bin albero){ FILE *file_albero; file_albero = fopen(nome_file, "r"); assert(file_albero); LeggiSottoAlbero(file_albero, 0, albero); fclose(file_albero);} /* LeggiAlbero */
/* stampa un elemento a un certo indice */void StampaIndice(int j,Tipo_albero_bin albero){ if (! albero[j].esiste) { printf("()"); return; } printf("( %d ", albero[j].info); StampaIndice(j*2 + 1, albero); StampaIndice(j*2 + 2, albero); printf(" )");} /* StampaIndice */
void StampaAlbero(Tipo_albero_bin albero){ StampaIndice(0, albero);} /* StampaAlbero */
La rappresentazione
mediante lista doppia
Esiste una corrispondenza fra il tipo astratto albero binario ed il tipo astratto lista; la corrispondenza la possiamo cosi’ esprimere:
a) se A e’ vuoto, A viene rappresentato dalla lista vuota;
b) se A non e’ vuoto, la lista che lo rappresenta e’ formata da tre elementi, il primo e’ un atomo e rappresenta la radice R di A; il secondo e’ una lista che rappresenta con lo stesso metodo, il sottoalbero sinistro di A ed il terzo e’ ancora una lista che rappresenta il sottoalbero destro di A.
Usando la rappresentazione parentetica usate per le liste avremo che il nostro albero binario di fig. 21.8 puo’ essere cosi’ espresso:
(A (B(D ()())(E()()))(C()(F()())))
Rappresentazione
mediante struct e puntatori
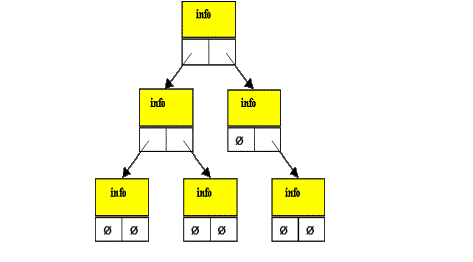
La fig. 21.8 e’ la rappresentazione grafica di un albero binario, rappresentato con struct e puntatori.
Infatti avendo un nodo di albero binario al massimo due figli, si utilizza il tipo struct con un campo per rappresentare la info del nodo e altri due campi in cui si memorizza il puntatore al sottoalbero sinistro in uno ed un altro in cui si memorizza il puntatore al sottoalbero destro.
typedef enum{TRUE=1,FALSE=0}Booleano;
typedef char Tipo_atomi;
struct Struct_albero_bin{
Tipo_atomi info;
struct Struct_albero_bin *punt_sin;
struct Struct_albero_bin *punt_des;
};
typedef struct Struct_albero_bin Tipo_nodo_albero;
typedef Tipo_nodo_albero *Tipo_albero_bin;
Vediamo di tradurre in linguaggio C le due funzioni di visita in preordine ed in postordine supponendo di avere definito la seguente funzione Analizza():
/* analisi del nodo: esempio la stampa */ void Analizza(char nodo){ printf("%c ", nodo);} /* Analizza */
/* visita in preordine dell'albero */void VisitaPreordine(Tipo_albero_bin A){ if (A == NULL)return;
Analizza(A->info); /* analizza la radice */
VisitaPreordine(A->sinistro); /* analizza il sottoalbero sinistro */
VisitaPreordine(A->destro); /* e poi il destro */
}
/* visita in postordine dell'albero */void VisitaPostordine(Tipo_albero_bin A){ if (A == NULL)return;
VisitaPostordine(A->sinistro);/* analizza il sottoalbero sinistro */
VisitaPostordine(A->destro); /* poi il destro */
Analizza(A->info); /* analizza la radice */
}
Gli alberi binari di ricerca
Definiamo albero binario di ricerca un albero binario A, in cui ogni nodo x ha la seguente proprieta’: tutti i nodi del sottoalbero sinistro di x hanno un valore minore od uguale del valore del nodo x e tutti i nodi del sottoalbero destro hanno un valore maggiore di quello del nodo x.
Scriviamo adesso una funzione che ricerca il valore elem all’interno dei nodi dell’albero binario di ricerca A; il valore ritornato dalla funzione e’ TRUE se elem e’ presente in A altrimenti e’ FALSE. Se elem e’ presente il puntatore punt_pos punta al sottoalbero di A la cui radice e’ pari ad elem.
Booleano
Ricerca(Tipo_albero_bin A,Tipo_atomi elem, Tipo_albero_bin *punt_pos)
{
Booleano
trovato;
if(A==NULL)
trovato=FALSE;
else
if(elem==A->info)
{
*punt_pos=A;
trovato=TRUE;
}
else
if(elem<A->info)
trovato=
Ricerca(A->punt_sin,elem,punt_pos);
else
trovato=
Ricerca(A->punt_des,elem,punt_pos);
return trovato;
}
__________________________________________________