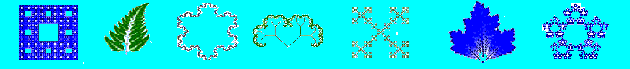
I  Frattali (*)

 

A prima vista, le figure note col nome un po’ bizzarro di frattali sembrano niente di più che degli oggetti dai contorni fortemente frastagliati. La loro natura di forme intrin­secamente complesse esse la rivelano solo quando si tenta, ingrandendole, di esaminarne più da vicino la frontiera.

 

Normalmente, quando si ingrandisce il contorno irregolare di un oggetto, specie se si tratta di ima forma definita matematicamente, ci si aspetta di vedere le asperità addolcirsi man mano che aumentiamo l’ingrandimento, finché esse cedono il posto ad una sinuosità regolare, che solo la discrepanza di scala faceva sembrare una irregolarità. Nulla di ciò accade con i frattali: al contrario, ogni cambiamento di scala rivela nuove e inaspettate concrezioni, in una. gerarchia di minuzie sempre più sottili. Quello che sembrava solamente un profilo frastagliato mostra ad uno sguardo più ravvicinato una struttura fine estremamente variegata, a sua volta destinata a ramificarsi ulteriormente ad ogni successivo ingrandimento. L’irregolarità dei frattali è infinitamente stratificata. A dispetto della estrema varietà di forme, la generazione di molti di questi oggetti è particolarmente semplice, e richiede al computer un programma di poche righe.

Immaginiamo una polvere posta su una superficie piana, le cui particelle si possono spostare come si vuole su questa superficie, restando ferme una volta che abbiamo finito di muoverle. Distribuendo questa materia diversamente da come era disposta all’origine, abbiamo operato una  trasformazione del piano, alla fine della quale la particella che

occupava il punto P si trova in una nuova posizione, che indicheremo con T(P) per ricordarci che si tratta del trasformato di P.

Ad esempio, se P è individuato dalle sue coordinate cartesiane (x, y), potremo descrivere la trasformazione T dicendo quali sono le coordinate (x₁,y₁) del punto T(P), coordinate che naturalmente dipenderanno da quelle di P:

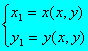
Supponiamo ora di operare una seconda volta la trasformazione T. La particella che originariamente era in P e che era stata spostata in T(P) andrà ora a finire in im nuovo punto T(T(P)), ovvero T²(P). Trasformando di nuovo, e poi ancora, il punto continuerà a muoversi in T³(P), T⁴(P), e così via, per finire, dopo un numero m di trasformazioni, in T^m(P).

 

Fissiamo ora un cerchio W di raggio abbastanza grande e poniamoci il seguente problema:

 

 dopo quante ripetizioni la particella inizialmente in P uscirà da O?

 

 Naturalmente, la risposta dipenderà dalla posizione iniziale P della particella. Ci sono ampie zone a partire dalle quali la particella esce da O quasi subito, mentre altri settori del piano saranno invece particolarmente tenaci, nel senso che non vedremo la particella uscire da O entro il numero massimo di iterazioni che abbiamo fissato.

 

Questo è il caso degli esempi più semplici di insiemi di Julia, che si ottengono da trasformazioni T dotate di un solo punto fisso attrattivo P_o  tutti i punti sufficien­temente vicini a Po vengono spostati in punti ad esso ancora più vicini, mentre tutti i punti sufficientemente lontani dall’origine vengono spostati in punti ancora più lontani.

 

In questa situazione tutti i punti del piano che non sono punti fissi di T cadranno in tre gruppi distinti: quelli che le cui immagini mi allontanano indefinitamente, quelli le cui immagini si avvicinano a Fo e gli altri, quelli che non hanno nessuno dei due compor­tamenti e che separano le due zone. Questo ultimo insieme di punti costituisce l’insieme di Julia della trasformazione, e per una scelta abbastanza ampia di trasformazioni ha una struttura frattale.

 

Per avere un’idea ditale struttura possiamo operare nel seguente modo. Fissata una regione limitata W del piano, che contiene tutto l’insieme dei punti attratti da Po, per ogni punto P di W calcoliamo un numero sufficientemente alto di iterazioni della trasformazione, e coloriamo il punto di partenza con un colore diverso a seconda del numero di iterazioni necessarie ad uscire da W, scegliendo ad esempio il colore W (nero) per i punti che rimangono confinati in W.

 

Come ci si può aspettare, se un punto P richiede N (diciamo 50) iterasioni per uscire da W, i punti vicini  a P richiederanno un numero di ripetizioni vicino a 50 (ad esempio fra 45 e 55). Quando però ci spostiamo in zone caratterizzate da un N via via più alto vediamo che il numero di iterazioni varia sempre più rapidamente passando da un punto ad un altro vicino. Si formano così delle figure molto frastagliate, in cui i colori ai mescolano in forme imprevedibili, ma mai in maniera casuale: c’è del metodo in questa follia. Da queste figure sempre nuove e inaspettate deriva la bellezza dei frattali.

 

(*) Tratto dalla mostra “Oltre il compasso”